Анатолий Молчанов - Население Земли как растущая иерархическая сеть II

Из всех существующих исторических циклов эндогенного и экзогенного характера будут рассмотрены только волны Кондратьева и сокращающиеся по закону прогрессии исторические циклы. Их мы считаем главными, основными циклами Мир-системы.

Прежде всего, введем две важнейшие для мировой истории даты: первая – это момент начала неолита, возьмем (условно, конечно, т. к. время начала первого исторического периода известно с некоторой точностью) за эту дату 8154 год до н. э. Почему неолит?

Потому что это начало мировой истории (что считается наиболее общепризнанным), т. е. именно в этот момент времени начинается мировой исторический процесс и процесс взрывного гиперболического роста населения Земли.

Вторая дата – это такой момент времени Т 0, при котором знаменатель в формуле Фёрстера обращается в нуль – так называемая точка сингулярности эмпирической гиперболы демографического роста.

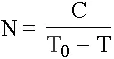
Рис. 1. Гипербола демографического роста населения Земли.

Здесь С – постоянная Фёрстера, равная 189,6·10 9лет, а Т 0= 2022 год [20]– дата, при приближении к которой численность населения Земли устремляется к бесконечности при условии неизменности закона роста. В шестидесятом году прошлого века, когда Фёрстер и его коллеги проводили свое исследование, демографический переход еще не начался и возможность катастрофического перенаселения Земли к 2022 году казалась вполне реальной.

Эта дата – 2022 год, полученная в результате математической экстраполяции и определенная с погрешностью в несколько лет, имеет для глобального исторического процесса значение не меньшее, чем момент начала неолита. Почему это так?

Во-первых,потому, что в этот момент времени, очевидно, перестает выполняться остававшийся неизменным в течение многих тысяч лет закон гиперболического роста населения Земли. На самом деле отклонение от гиперболического роста было зафиксировано за несколько десятилетий лет до этого момента, но дата Т 0, несомненно, играет важную роль, т. к. вместе с постоянной Фёрстера полностью определяет эмпирическую гиперболу демографического роста.

И, во-вторых,во второй половине двадцатого столетия начался глобальный демографический переход: явление, хорошо изученное для отдельных, прошедших свой «локальный» переход стран. Переход, истинная причина которого – называются десятки причин – до сих пор остается непонятной и даже загадочной. Несомненно только то, что является он глобальным, т. е. это согласованный для всех стран и народов процесс; происходит он в XX – XXI вв., причем численность населения Земли в момент его завершения стабилизируется и расти больше не будет.

Существуют различные прогнозы роста численности человечества на ближайшие сто и двести лет. Любой не катастрофический прогноз предполагает ее стабилизацию на некотором фиксированном уровне, определяемом ресурсами и экологией. Наиболее логичной представляется стабилизация, происходящая сразу после перехода, поскольку численность населения ряда стран Европы и Америки, уже прошедших свой «локальный» демографический переход, больше не растет и (в первом приближении) не уменьшается. Несомненно также и то, что явление это не только демографическое, но также социальное и историческое.

Итак, существуют две важнейшие даты мировой истории: момент начала неолита (и начала взрывного гипеболического роста), когда по всей Ойкумене происходит, причем по историческим меркам мгновенно, переход от охоты и собирательства к скотоводству и земледелию.

И точка сингулярности эмпирической гиперболы демографического роста, определяющая момент окончания длившегося тысячелетиями гиперболического роста населения Земли и время прохождения глобального демографического перехода. Назовем эту демографическую и историческую сингулярность сингулярностью Дьяконова – Капицы.

Отметим также, что обе эти даты – реальные исторические вехи, не связанные ни с какими теориями. За момент начала неолита берем 8154 год до н. э., время Т 0положим равным 2022 году; постоянную Фёрстера примем равной 189,6·10 9лет.

Для дальнейшего нам понадобятся некоторые сведения из элементарной математики. Гипербола y = 1/x обладает тем очевидным свойством, что при уменьшении ее аргумента в два раза, ее значение возрастает в два раза. Геометрическая прогрессия со знаменателем ½ обладает одной особенностью, выделяющей ее среди других прогрессий.

Она заключается в том, что каждый последующий ее член, будучи отмечен точкой на числовой оси, есть середина отрезка, соединяющего точку, изображающую предыдущий член и точку, представляющую предел общего члена прогрессии (точку нуль).

Иначе говоря, члены этой прогрессии можно отметить последовательностью шагов по числовой оси, в которой каждый последующий шаг вдвое короче предыдущего. Пусть теперь аргументами гиперболы будут члены геометрической прогрессии, с первым членом равным единице и знаменателем ½:

Рис. 2. Прогрессия и гипербола.

Тогда последовательность значений аргумента будет составлять бесконечно убывающую прогрессию со знаменателем ½, а последовательность значений функции, соответственно, – бесконечно возрастающую прогрессию со знаменателем равным двойке. Произведение x·y будет при этом оставаться постоянным и равным единице. Построим график y(x) = 1/x (ось 0X направим влево, ось 0Y – вверх).

Если перейти к системе координат с началом сдвинутым на единицу в положительном направлении оси 0Х, а саму эту ось обратить (направить вправо), то уравнение гиперболы примет вид: y'(x') = 1/(1-x'). Последовательность точек на числовой оси, которая в исходной системе координат определялась бесконечно убывающей прогрессией, в преобразованной системе задается последовательностью сумм этой прогрессии.

Применим эту математику для разбиения всей истории развития человечества от неолита до наших дней. Формула гиперболы мирового демографического роста имеет вид:

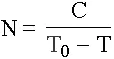
Рис. 1. Гипербола демографического роста населения Земли.

Где Т 0= 2022 + 8154 = 10176 год – дата сингулярности, если время отсчитывать от начала неолита, С – постоянная Фёрстера, равная 189,6·10 9лет.Составим теперь последовательность времен по следующему правилу, которое назовем алгоритмом восьми шагов:

• Во-первых, все времена будем отсчитывать от момента начала неолита, и первый член этого ряда положим равным нулю;