Том ДеМарко - Вальсируя с медведями

Как бы вы это ни сделали, фигура из выбранных точек должна, в конечном счете, повторять изначальную диаграмму неопределенности. Чтобы проверить себя, вы можете собрать свои результаты за некоторый период времени, рассортированные по удобным группам, и использовать их для построения гистограммы своих выбранных результатов. Если вы правильно рассчитали процесс выборки, последовательные гистограммы (для все большего и большего числа элементов выборки) могли бы выглядеть так:

В итоге, когда вы наберете пару сотен точек, огибающая вашей гистограммы будет очень похожа на диаграмму неопределенности, с которой вы начали:

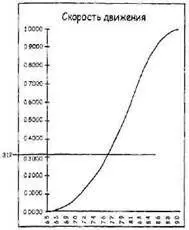
Выборка Монте-Карло — это подход, гарантирующий соблюдение формы наблюдаемой кривой во времени. Механизм выбора Монте-Карло использует данные прошлых наблюдений в форме кумулятивной диаграммы неопределенности вместе с простым генератором случайных чисел для отбора. Если выбрать достаточное количество данных, гистограмма этой выборки начнет аппроксимировать фигуру ваших наблюдаемых данных. Генератор настроен на выдачу случайных чисел между 0 и 1. Вся штука в том, чтобы использовать сгенерированное число для выбора значения на вертикальной оси диаграммы неопределенности и проведения через него горизонтальной линии. Если, например, первое сгенерированное число было 0,312, вы рисуете горизонтальную линию, проходящую через точку 0,312 на вертикальной оси (см. верхний рисунок на следующей странице).

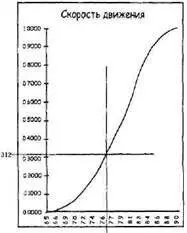
Затем вы проводите вертикальную линию через точку, где ваша горизонталь пересекает кривую. Соответствующая величина на горизонтальной оси — это ваша первая точка выборки (см. нижний рисунок на следующей странице).

Второй рисунок говорит о том, что для первого выборочного забега вокруг площадки можно ожидать скорость 7,66 миль/час. Теперь повторим это, взяв больше случайных чисел, каждое из которых дает выборочное значение скорости. Если достаточно долго продолжать этот процесс и построить из результатов гистограмму, то огибающая гистограммы начнет аппроксимировать диаграмму неопределенности, с которой вы начали (ее дифференциальный вид).

Механизм выборки, построенный на таком простом правиле, можно теперь применить к проблеме бега. Нам понадобится два таких механизма: один для получения данных с диаграммы скорости и другой для получения данных с диаграммы расстояния:

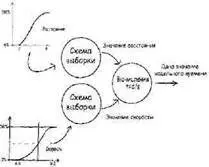
Этот подход позволяет обходиться арифметическими действиями с выборками, вместо интегрального исчисления по кривым. В первый раз, когда вы запускаете этот процесс, он говорит вам, что вы пробежите, скажем, за 33 минуты. Этот результат не так уж и значим — это просто рассчитанное время для случайно выбранных величин из диапазона разброса скорости и расстояния. Но повторение этого процесса снова и снова даст распределение результатов, которые начинают аппроксимировать неопределенности ожидаемого времени забега.

Диаграмма, показанная выше, — это симулятор Монте-Карло для проблемы двойной неопределенности. Он позволяет вам моделировать n случаев проблемы и отображать результаты в форме результирующей диаграммы неопределенности. Вот результат для 100 образцов:

Метод, использованный здесь, не ограничен двумя неопределенностями. Его можно использовать для всего портфеля рисков, грозящих проекту по созданию программного обеспечения.

«RISKOLOGY» — это симулятор Монте-Карло, созданный для менеджера, занимающегося рисками в проекте по разработке программного обеспечения. Это — прямое воплощение механизма выборки по методу Монте-Карло, выраженное в терминах логики электронных таблиц. Мы написали эту программу в Excel, поэтому вам понадобится лицензионная копия программы, чтобы использовать этот инструмент. «RISKOLOGY» идет в комплекте с нашими собственными данными о некоторых рисках, с которыми может столкнуться ваш проект. Вы можете использовать наши данные или заменить их собственными.

Скачайте копию симулятора «RISKOLOGY» с нашего сайта: http://www.pmo.ru/riskology

Там же можно найти некоторые шаблоны и инструкции по использованию и подгонке симулятора.

Как только вы смоделировали достаточное количество примеров для своего проекта, симулятор обеспечит вам достаточно гладкую результирующую кривую. Эта кривая может показывать совокупные риски, связанные со сроком сдачи вашего проекта или с набором функциональных качеств, которые могут быть готовы к заданному сроку. В терминах управления рисками, результат представляется как диаграмма совокупного риска.

Для незнакомых с управлением рисками, или тех, кому очень сложно понять неопределенность, мы предлагаем воспринимать это как результат моделирования: «Мы прогнали этот проект 500 раз через симулятор, и получили результат, показанный на рисунке».

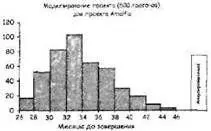
«Как вы видите, это показывает, что мы закончим работу до конца 30-го месяца проекта только в 15% случаев, — говорите вы. — Это не значит, что дата недостижима, она всего лишь имеет высокие риски. На нее можно рассчитывать лишь с 15%-ной уверенностью. Если вам нужна 75%-ная уверенность, вам лучше объявить датой сдачи 40-й месяц».

Наш симулятор «RISKOLOGY» не является единственным вариантом решения этой задачи. Существуют в продаже и другие подобные продукты. Вместо того, чтобы давать здесь прямые указания, мы будем поддерживать список на нашем сайте «RISKOLOGY» (см. URL выше). Там есть описания еще, по крайней мере, двух инструментов — наборов для построения своих собственных симуляторов риска. Эти продукты недороги, и их весьма легко освоить. Далее, как было обещано, мы перейдем к тому, что считаем самыми распространенными ключевыми рисками, с которыми сталкиваются руководители проектов по разработке программного обеспечения.