Геннадий Горелик - Кто изобрел современную физику? От маятника Галилея до квантовой гравитации

g(R) = GM/R 2 ,

здесь G — константа, одинаковая для любого небесного тела, а значит, константа фундаментальная.

Как Галилей мог открыть общий закон свободного падения

Исследуя свободное падение, Галилей выяснил, что шар, брошенный горизонтально в пустоте, падает по параболе, форма которой определяется начальной скоростью V и ускорением свободного падения g : при этом скорость движения по горизонтали сохраняется V г = V , а по вертикали растет со временем V в = gt .

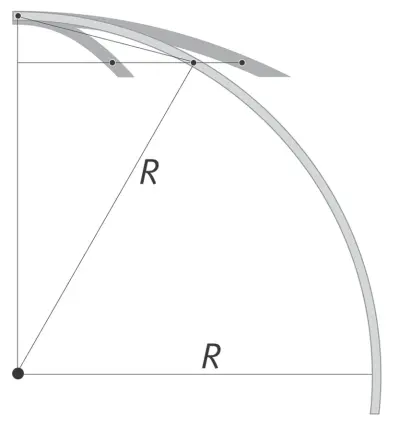
Сделаем мысленный эксперимент, поднявшись вместе с мысленным Галилеем на легендарную башню. Будем бросать шары горизонтально со все большей скоростью. Если скорость броска мала, шар упадет — по крутой параболе — на землю поблизости от башни. А если скорость очень велика, парабола станет очень пологой, и шар улетит очень далеко от Земли.

Спрашивается, с какой скоростью надо бросить шар, чтобы, свободно падая, он оставался на той же высоте от земной поверхности, уходящей закругленно «вниз»?

На этот вопрос ныне может ответить и школьник, нарисовав указанную схему, применив теорему Пифагора и учтя, что радиус Земли R ≈ 6000 км, а ускорение свободного падения g ≈ 10 м/сек 2. Эти величины, как и теорему Пифагора, знал также и Галилей. И мог получить, что искомая скорость связана с g и R соотношением

V 2 = gR

и равна примерно 8 км/сек. Летя с такой скоростью, шар оставался бы на постоянном удалении от земной поверхности. Совсем как Луна.

Однако Галилей легко обнаружил бы, что лунные величины R л ≈ 400 000 км и V л≈ 1 км/сек никак не укладываются в полученное соотношение. А чтобы уложились, нужно значение g л, примерно в 3600 раз меньшее измеренного Галилеем на поверхности Земли . Расстояние до Луны больше радиуса Земли примерно в 60 раз, а 60 60 = 3600. Отсюда Галилей мог предположить, что ускорение свободного падения g меняется с удалением от Земли обратно пропорционально квадрату расстояния R :

g ~ 1/ R  2 .

Отсюда, с учетом предыдущего соотношения, следует, что скорость спутника меняется с расстоянием R от небесного тела:

V ~ 1/ R  1/2 .

А если небесное тело имеет несколько спутников, то для них всех величина VR  1/2одна и та же.

Подтвердить это свойство Галилей мог на им же открытых спутниках Юпитера:

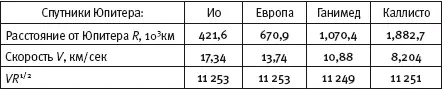
Подтвердили бы это и спутники Солнца, то есть планеты (орбиты которых близки к круговым).

Так закон свободного падения, установленный в земных физических опытах, поднялся бы до астрономических высот. И так Галилей пришел бы к новому закону природы, который мог назвать общим законом свободного падения : ускорение свободного падения на расстоянии R от центра небесного тела

g(R) = A/R  2 ,

где А — некая константа, определяемая свойствами небесного тела.

Из наблюдательных данных Галилей мог вычислить соотношения таких констант для Земли, Юпитера и Солнца:

A Юпитера ≈ 300 A Земли ,

A Солнца ≈ 300 000 A Земли .

Глядя на эти три величины, характеризующие Землю, Юпитер и Солнце, естественно было спросить, какие различия небесных тел ведут к различиям их констант A . Из явных различий в размере, в количестве вещества (массе) и в состоянии светимости легче всего предположить, что величина A пропорциональна массе небесного тела M: A = GM с неким коэффициентом G (который тоже можно грубо оценить, считая среднюю плотность Земли близкой к плотности ее твердых пород).

В результате Галилей получил бы общую зависимость сразу для всех трех небесных тех — Земли, Юпитера и Солнца:

g (R) = GM/R  2 ,

и здесь константа G — не простая, а фундаментальная, поскольку одинакова для Земли, Юпитера и Солнца и, судя по этому, для любого другого тела.

Это и есть общий закон свободного падения, открыть который вполне мог Галилей на его уровне знаний и умений.

Новый закон уже намекает на гравитацию Ньютона, до которой оставалось более полувека. Но для Галилея всего важнее было бы оправдание его веры в физическое единство мира — и мира подлунного, и мира надлунного. Он понял бы, что причина падения тел на Земле и причина, определяющая орбиты планет, — одна и та же. А поскольку причину падения естественно называть притяжением (к Земле), то так можно назвать и планетную силу. Мысленный спутник Земли помог бы Галилею увидеть, что свободное падение и движение планет — явления глубоко родственные.

Так он понял бы, что слова Кеплера о планетно-солнечных притяжениях не столь и ребяческие. Никакой солнечной силы, движущей планетами, конечно, нет, но притяжение есть и подчиняется вполне определенному закону. Более того, из этого закона следует и (третий) закон Кеплера, связывающий время, за которое планета проходит свою орбиту, с ее радиусом (T 2 ~ R 3 ) . Значит, из закона свободного падения, установленного в земных физических опытах, следует астрономический закон, полученный Кеплером в результате многолетнего анализа множества астрономических наблюдений. Следует пока лишь для круговых орбит. Но если ускорение свободного падения известно в каждой точке пространства вокруг большого небесного тела, то можно и ставить задачу о том, как изменится круговая орбита спутника, если его толкнуть. Труднее, конечно, было заподозрить и тем более доказать, что при этом окружность превратится в эллипс. Но зато теперь Галилей мог уже принять подсказку первого закона Кеплера — об эллиптичности планетных орбит, к великой радости автора и к успокоению историков, ломающих головы над молчанием Галилея по поводу законов Кеплера.

Имея в своем распоряжении мысленный спутник, Галилей вряд ли бы остановился на достигнутом, а понял бы также, что законы Кеплера… лишь приближенные. Запуская мысленный спутник на разных расстояниях от Земли, легко дойти до места посередине между Землей и Марсом. А тогда возникнет вопрос: мы запускаем спутник Земли или Марса? Владея понятием составного движения, Галилей «сложил» бы оба ускорения свободного падения с учетом разных направлений (нынешними словами — векторно) и получил бы суммарное движение, совсем не похожее на эллипс. Отсюда следовало бы, что законы Кеплера — приближенные, они тем точнее, чем дальше находятся все массивные тела от одного, «центрального». И возникла бы общая задача о движении «спутника» вблизи нескольких массивных тел. Все это вело к представлению о всеобщем — «всемирном» — притяжении. Но оно уже было бы основано не на словах полуастрологического происхождения, как у Кеплера, а на физическом исследовании свободного падения вблизи поверхности Земли.