Александр Помогайбо - Тайны великих открытий

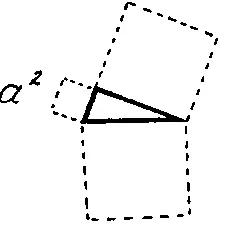
Теперь попытаемся связать геометрическое толкование теоремы Пифагора и алгебраическое ее выражение. Что, к примеру, обозначает а 2? Чтобы подсознание ответило на этот вопрос, мысленно поставим перед собой как а 2, так и геометрическое представление теоремы — и задаемся вопросом: что обозначает а 2?

Через несколько мгновений мозг выдает мелькнувший — и неуловимый — зрительный образ, после чего в голове словно звучат слова: "площадь квадрата со стороной а". Мгновением позже мозг выдает и "ссылку" — рисунок, в котором автор этих строк определял площадь под кривой на зачете по физике в институте (это, видимо, и мелькнуло). Таким образом, четко представленный образ и четко сформулированный вопрос позволили мозгу быстро отыскать аналог.

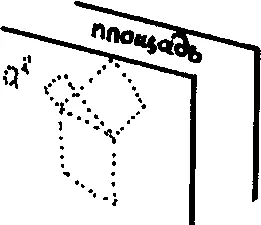
Отложим для себя на отдельный гипотетический листочек понятие "площадь" — оно нам, по-видимому, может пригодиться.

А что обозначают а 2и b 2? Представляем их зрительно:

Ответ приходит через доли секунды — "тоже площади".

Значит, ключевой геометрический "принцип" теоремы Пифагора — соотношение площадей. Это соображение рождает мысль — искать доказательство через площади. (Эта мысль появилась опять благодаря тому, что мы четко сформулировали исходные данные — но на сей раз уже не в виде образа, а в виде предложения.)

Но как связать площади? Мозг: "Их все связывает треугольник".

Зрительно проанализируем общую картинку — добавив понятие площади.

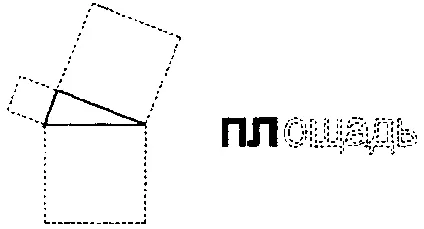
В голове слышится голос: "А если рассмотреть такую площадь?" — и вспыхивает картинка:

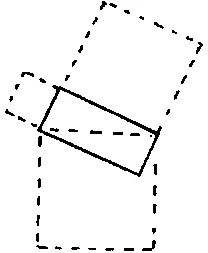
Эту трансформацию образа, опять-таки, осуществил наш мозг.

А как определить площадь этой фигуры?

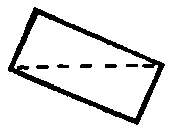
Из зрительной картинки сразу видно — "а" надо умножить на "b". А как выразить площадь через "с"?

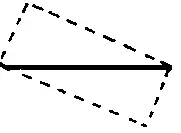
Из картинки это не видно.

Мозг: "Может, стоит вернуться к треугольнику?"

Нет, чего-то тут не хватает. Чего? Мозг выдает следующее:

Мозг "дорисовывает" картинку. Опять же, "добавляя" ссылку на какую-то задачу по геометрии в шестом классе.

Как обозначается высота? Перед мысленным взором вспыхивает:

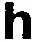
Но высота нам не дана. Как быть? Концентрируемся некоторое время на мысленной картинке:

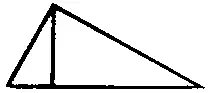
В голове смутно вырисовывается какая-то картинка. Не очень напрягаемся, чтобы ее не вспугнуть, но стараемся от нее не отвлекаться. Вот она выходит, становится яснее… и, когда часть ее уже вырисовалась, в голове возникает мысль: когда один из элементов неизвестен, его можно вычислить по соотношениям. Картинка становится еще четче, и теперь понятно, почему она "задержалась", картинки две, и они мешали друг другу. Одна — чертеж прямоугольника с подобными сторонами из уроков геометрии, другая — формула пропорций, по которой вычислялось содержание вещества на уроках химии.

Итак, надо использовать треугольник с подобными сторонами. С этой мыслью внезапно возникает и предвкушение правильного решения, пробуждающее положительные эмоции.

После того как найден главный принцип, начинается чисто механическая работа — определение пропорций (это можно уже делать и на листе бумаги).

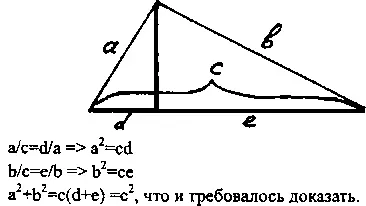
Итак, формулируем основные принципы решения такого рода задач.

1. Четкая формулировка задачи (достигается логикой).

2. Максимально четкое воспроизведение перед умственным взором отдельного, самого простого, элемента понятия (достигается визуализацией).

3. Удержание мысленного образа перед умственным взором при одновременном удержании в голове вопроса.

4. Когда вспыхивает ответ, следует оценка его, выявление неясностей.

5. Четкая формулировка неясностей и максимально четкое представление элемента, в котором есть неясность (опять же, этот элемент должен быть как можно меньшим).

На мысленном "отдельном листочке" полезно фиксировать промежуточные выводы, которые могут быть полезными.

Визуализацию использовало великое множество выдающихся деятелей науки. Визуализация — непременный элемент работы художника, особенно тех, кто рисует не с натуры (как делал, к примеру, Айвазовский). Использовали визуализацию даже музыканты (Скрябин видел музыку в цвете) и поэты (судя по многочисленным рисункам на полях).

Александр Куприн использовал два метода зрительного воображения. Первый заключался в том, что писатель мысленно наблюдал жизнь своих героев как бы со стороны. Второй — в том, что он мысленно сам "включался" в действие. А. Куприн считал его более эффективным.

Судя по всему, Максим Горький использовал нечто похожее на второй метод. Однажды писателя нашли почти в обморочном состоянии — он описывал, как в его героя вонзили нож.

Никола Тесла в детстве развил в себе искусство визуализации самостоятельно и в школьные годы производил все математические вычисления на мысленно представленной классной доске, почти мгновенно называя конечный результат.

Обычно при решении научных задач с помощью визуализации в голове создается образ как исходных данных, так и вопроса.

Тогда часто задача решается словно сама собой (но мы-то знаем, что это неутомимое подсознание раскапывает в нашей памяти аналоги!).

В большинстве случаев задача не выглядит идеальной моделью. Потому сначала требуется проделать большую работу по определению действительно необходимых данных. К примеру, до Галилея никому не пришло в голову пренебречь трением.