Наум Виленкин - В поисках бесконечности

Мы занумеровали, таким образом, все положительные рациональные числа. А теперь уже легко понять, как нумеруются все (то есть положительные и отрицательные) рациональные числа. Для этого надо записать их отдельно в виде двух таблиц и числа одной таблицы нумеровать четными номерами, а второй — нечетными (и еще оставить один номер для нуля).

Вообще, складывая счетное множество счетных множеств, мы снова получим счетное множество. Это доказывается тем же самым приемом нумерации по квадратам.

Нам удалось занумеровать все рациональные числа. Но рациональные числа получаются из натуральных чисел с помощью лишь одной операции — деления (и еще, быть может, изменения знака). А теперь мы добавим еще операцию извлечения корня и будем рассматривать все числа, которые можно получить из натуральных чисел с помощью этой операции и арифметических действий. Среди этих чисел будут такие, как 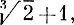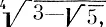и даже такие "монстры", как

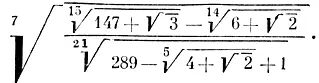
Возникает вопрос: можно ли занумеровать множество всех таких чисел? Это кажется еще более трудным, чем занумеровать множество рациональных чисел. В самом деле, какому числу надо приписать меньший номер: 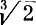или 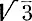? Но оказывается, что и это множество счетно, то есть его элементы можно перенумеровать.

Чтобы доказать это утверждение, отметим сначала, что каждое число рассматриваемого вида является корнем алгебраического уравнения вида

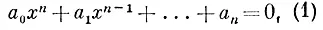
где a 0≠0 и a 0, ..., a n— целые числа. Например, 3/ 7— корень уравнения 7x — 3 = 0, 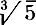— корень уравнения x 3— 5 = 0, а 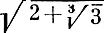— корень уравнения x 6— 6x 4+ 12x 2— 11 = 0. Иногда бывает очень трудно написать уравнение, которому удовлетворяло бы число описанного выше вида, но тем не менее это всегда возможно.

Заметим, что далеко не все корни уравнений вида (1), где a 0,..., a n— целые числа, выражаются через натуральные числа с помощью арифметических действий и операции извлечения корня. Например, корни уравнения

x 5— 3x + 3 = 0

нельзя выразить в таком виде, оно, как говорят, не решается в радикалах. Все числа, являющиеся корнями уравнений вида (1) с целыми коэффициентами, называют алгебраическими числами. Таким образом, множество алгебраических чисел содержит в себе множество всех чисел, выражаемых через натуральные с помощью арифметических действий и извлечений корней. Поэтому если нам удастся перенумеровать все алгебраические числа, то тем более мы решим задачу, поставленную в начале этого пункта.

Но прежде чем нумеровать алгебраические числа, надо перенумеровать сами алгебраические уравнения вида (1), А тогда задача будет уже решена. Ведь каждое алгебраическое уравнение n-й степени имеет не более n корней. Поэтому после того, как все уравнения с целыми коэффициентами будут перенумерованы, мы составим таблицу, в первой строке которой будут все различные корни первого уравнения, во второй — все различные корни второго уравнения, не попавшие в первую строку, в третьей- все различные корни третьего уравнения, не попавшие в первую или вторую строку, и т. д. Таблица получится такая:

Теперь ясно, как нумеруются все числа этой таблицы (порядок нумерации указан стрелками).

Итак, займемся нумерацией множества алгебраических уравнений с целыми коэффициентами. Для этого применим идею, с помощью которой пробовал решить самую трудную задачу директор гостиницы. Напомним, что он предложил воспользоваться числами вида 2 m3 n. Чтобы решить нашу задачу, придется использовать все простые числа. Читатель, конечно, помнит, что любое натуральное число единственным образом представляется в виде произведения простых множителей.

Поступим следующим образом. Сначала перенумеруем все целые числа (это мы уже умеем делать). Номер целого числа a обозначим через a. Каждому уравнению вида a 0x n+ a 1x n-1+ ... + a n= 0 (где, напомним, a 0,..., a n— целые числа) поставим в соответствие число

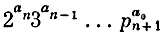
(через p n+1здесь обозначено (n-+1)-е простое число). Например, уравнению 3x 2— 2 = 0 ставим в соответствие номер 2 43 15 6= 150 000, потому что целое число -2 имеет номер 4, нуль — номер 1, а целое число 3 — номер 5. Теперь каждое уравнение получило свой номер, причем разным уравнениям соответствуют разные номера (каждый номер N единственным образом разлагается на простые множители, то есть единственным образом задает числа a n, a n+1,..., a 0; этим же числам соответствуют определенные целые числа a n , a n-1 , ..., a 0 , а тем самым и определенное уравнение a 0x n+ ... + a n= 0).

Мы уже выяснили, что значат слова "два множества имеют поровну элементов".

А теперь выясним, что значит "одно множество имеет больше элементов, чем второе". Для конечных множеств это тоже можно выяснить, не прибегая к счету. Вспомним пример с танцплощадкой.

Если после того, как заиграет оркестр и юноши пригласят девушек танцевать, некоторые нерасторопные юноши окажутся не у дел, то ясно, что юношей больше. Если же часть девушек будет с грустью наблюдать за своими танцующими подругами, то ясно, что больше девушек.

В этих случаях мы поступали так: устанавливали взаимно однозначное соответствие между одним множеством и частью другого множества. Если это удавалось, то отсюда следовало, что второе множество содержит больше элементов, чем первое. Пользуясь этим методом, легко установить, например, что рыб в океане меньше, чем атомов на земном шаре (хотя оба эти множества и конечны, их вряд ли возможно пересчитать). Для этого достаточно каждой рыбе поставить в соответствие один атом, входящий в состав ее тела. Тем самым будет установлено взаимно однозначное соответствие между множеством всех рыб и частью множества всех атомов на земном шаре.

К сожалению, для бесконечных множеств так просто поступить нельзя. Ведь мы уже видели, что множество может иметь столько же элементов, сколько и его часть. Поэтому только из того, что множество A имеет столько же элементов, сколько часть множества B, еще нельзя заключить, что оно имеет меньше элементов, чем все множество B.