Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

Следующей выдающейся фигурой той эпохи стал Галилео Галилей, открывший математические формулы движения маятника и падающих тел. В 1589 г., занимая должность профессора математики в Пизанском университете, он проводил эксперименты по качению шара по наклонной плоскости, но не опубликовал результаты. Однако именно тогда он осознал важность контролируемого эксперимента для изучения законов природы: эта идея стала фундаментальной для науки. Он занимался астрономией и сделал несколько важных открытий, побудивших его признать теорию Коперника о гелиоцентрической планетарной системе. Это обострило его отношения с церковью, обвинившей ученого в ереси и посадившей под домашний арест.

В последние годы жизни, уже окончательно ослабев здоровьем, Галилей создал «Беседы и математические доказательства двух новых наук», где объясняется его работа по движению тел на наклонных плоскостях. Он утверждал, что расстояние, на которое прокатится с постоянным ускорением изначально неподвижное тело, пропорционально квадрату времени. Основой его закона стало более раннее открытие, что снаряд летит по параболе. В сочетании с законами Кеплера о движении планет это заложило основу новой области науки – механики , математического описания движения тел.

Вот так и вышло, что физико-астрономические предпосылки привели ученых к исчислениям. Далее мы познакомимся с их математической основой.

Изобретение исчисления стало результатом более ранних исследований внешне не связанных проблем, обладавших скрытыми общими чертами. Сюда входит определение мгновенной скорости движения объекта в любой заданный момент, определение касательной к кривой, измерение длины кривой, определение максимального и минимального значения переменных величин, нахождение площади любой фигуры на плоскости и объема любого тела в пространстве. Ряд важных идей и примеров были разработаны Ферма, Декартом и не столь известным англичанином, Исааком Барроу, но методы решения по-прежнему оставались частными для каждой отдельной задачи. Требовался обобщенный поход.

Галилео был сыном Винченцо Галилея, преподавателя музыки, использовавшего эксперименты со струнами для подтверждения своей теории. В десять лет Галилео отдали на обучение в монастырь Валломброза с перспективой сделать его медиком. Но он не интересовался медициной и всё свое время посвящал математике и натуральной философии, которую позже мы назовем естественной наукой.

В 1589 г. Галилео занял пост профессора в Пизанском университете. В 1591 г. его пригласили на более высокооплачиваемое место в Университете Падуи, где он преподавал евклидову геометрию и астрономию студентам-медикам. В то время врачи широко прибегали к астрологии для лечения пациентов, и обе науки являлись обязательной частью программы обучения.

Узнав об изобретении телескопа, Галилео собрал для себя такой прибор. Он настолько поднаторел в этом, что поделился своими наработками с Венецианским сенатом, пообещав ему эксклюзивные права на прибор в обмен на повышение гонораров. В 1609 г. Галилей постоянно наблюдал за небом, и одно открытие следовало за другим: четыре луны Юпитера, отдельные звезды внутри Млечного Пути, горы на Луне. Козимо де Медичи, великий герцог Тосканы, был так впечатлен телескопом, что сделал Галилея своим первым математиком.

Он открылсуществование пятен на Солнце и опубликовал свое открытие в 1612 г. К этому моменту собственные астрономические открытия убедили ученого в правоте теории Коперника, и в 1616 г. он публично выразил свое мнение в письме великой герцогине Кристине Лотарингской, утверждая, что теория Коперника отражает физическую реальность и это не просто практический способ упростить подсчеты.

На этот раз папа Павел V издал приказ инквизиции установить, верна или фальшива гелиоцентрическая теория, и инквизиторы признали ее ложью. Галилею приказали отказаться от теории, но на престол взошел новый папа, Урбан VIII, казавшийся более терпимым к этому открытию, и Галилей пренебрег запретом. В 1623 г. он опубликовал работу «Пробирных дел мастер» (итал. «Il Saggiatore»), посвятив ее Урбану. В этом труде мы находим его знаменитое утверждение, что Вселенная «написана на языке математики, и знаки ее – треугольники, окружности и другие геометрические фигуры, без которых нельзя понять ни единого из стоящих в ней слов и остается лишь блуждать в темном лабиринте».

В 1630 г. Галилейиспросил позволения опубликовать новую книгу, «Диалог о двух системах мира», – сравнительный анализ геоцентрической и гелиоцентрической теорий. Когда в 1632 г. пришло разрешение на публикацию из Флоренции (но не из Рима!), он издал книгу. В ней утверждалось, что главным доказательством движения Земли являются морские приливы. Теория Галилея о приливах оказалась ошибочной, но церковные иерархи сочли этот труд настоящей бомбой под своей властью. Инквизиция запретила книгу, а Галилея призвали в Рим, на суд по обвинению в ереси. Ученого признали виновным, но пожизненное заключение заменили домашним арестом. Ему повезло по сравнению со многими другими еретиками, для которых сожжение у столба стало обычным наказанием. Под домашним арестом Галилей создал «Беседы», в которых изложил свою теорию движения небесных тел. Ее контрабандой удалось вывезти из Италии и напечатать в Голландии.

Первый прорыв в этой области сделал Готфрид Вильгельм Лейбниц, юрист по профессии, посвятивший практически всю жизнь математике, логике, философии, истории и многим другим отраслям науки. Примерно в 1673 г. он начал работу над классической проблемой проведения касательной к кривой и обнаружил, что это обратная сторона проблемы измерения площадей и объемов. Последняя требовала найти кривую по заданной касательной, а первая подразумевала в точности обратное действие.

Воспользовавшись этой связью, в итоге Лейбниц сумел открыть то, что мы называем интегралами, используя сокращение omn (сокр. оmnia , лат. «всё»). В его бумагах можно найти такие формулы:

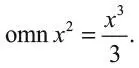
К 1675 г. он уже заменил omn на знак ∫, используемый и по сей день и представляющий собой вытянутую букву s, обозначающую сумму. Он работал с понятиями бесконечно малых приращений dx и dy для величин x и y и использовал их соотношение dy / dx для определения скорости изменения y как функции x . Получается, что если f – это функция, Лейбниц мог написать: