Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

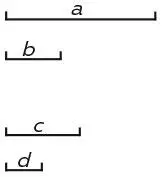
Равны ли соотношения a: b и c: d?

Такое определение требует специальных навыков, зато прекрасно вписывается в ограниченные возможности греческой геометрии. Так или иначе, оно работает; более того, оно позволило греческим геометрам взять теоремы, легко доказуемые с помощью рациональных отношений, чтобы расширить их действие до иррациональных.

Часто они использовали так называемый метод исчерпывания (или, иначе, истощения), в котором некоторые видят предка современного метода пределов и интегрального исчисления. Этим методом они доказали, что площадь круга пропорциональна квадрату его радиуса. Доказательство основывалось на простом факте, открытом Евклидом: площади двух подобных многоугольников соотносятся в той же пропорции, что и квадраты их соответствующих сторон. Круг представлял проблему: он не был многоугольником. Тогда греки построили две последовательности многоугольников: одну помещавшуюся внутри круга, а вторую – снаружи. Каждый следующий многоугольник всё ближе подходит к кругу, и из метода исчерпывания, доведенного до совершенства Евдоксом, следует, что площади самых близких к кругу многоугольников стремятся к его площади и в итоге совпадут с ней.

Самым известным греческим геометром, хотя, возможно, и не самым талантливым математиком, считается Евклид Александрийский. Он внес огромный вклад в историю науки, собрав труды предшественников и сведя их воедино, и его «Начала» – шедевр всех времен и народов. Евклид создал не меньше десяти трудов по математике, из которых до нас дошло только пять, и те в поздних копиях, в виде фрагментов. До наших дней не дожил ни один подлинный документ из Древней Греции. Пять имеющихся текстов Евклида называются «Начала», «О делении», «Данные», «Явления» и «Оптика».

«Начала» считаются основным трудом Евклида, который окончательно утвердил разделение геометрии на двумерную (планиметрию) и трехмерную (стереометрию). «О делении» и «Данные» содержат разные дополнения и комментарии в части геометрии. «Явления» посвящены астрономии, сферической геометрии и исследованию геометрических фигур на поверхности сферы. «Оптика» также относится к этой области и может считаться первой попыткой исследования геометрии перспективы – способности человеческого глаза преобразовать трехмерное изображение в двумерную картинку.

Пожалуй, лучшим трудом Евклида можно считать исследование логики пространственных отношений. Если форма имеет определенные свойства, логично, что они определяют и другие ее характеристики. Например, если у треугольника равны все три стороны, т. е. он равносторонний, то должны быть равны и все три его угла. Такой вид утверждений, когда делается допущение, а потом приводится его логическое следствие, называется теоремой. Здесь это теорема о свойствах равностороннего треугольника. Менее интуитивно понятна, зато более известна теорема Пифагора.

«Начала» состоят из 13 книг, выстроенных в логической последовательности. В них обсуждаются геометрия плоскости (планиметрия) и некоторые аспекты геометрии пространства (стереометрии). Важный момент – доказательство существования пяти геометрически правильных многогранников: тетраэдра, гексаэдра (попросту куба), октаэдра, додекаэдра и икосаэдра. Основные фигуры планиметрии – линия и круг, часто встречающиеся в разных сочетаниях: например, треугольник – сочетание трех прямых линий. В стереометрии мы имеем дело с плоскостями, цилиндрами и сферами.

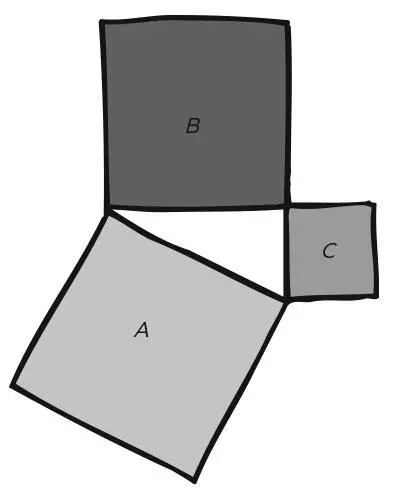
Теорема Пифагора: если треугольник прямоугольный, площадь большого квадрата А равна сумме площадей двух других, В и С

Для современных математиков представляет интерес не столько содержание трудов Евклида, сколько их логическая структура. В отличие от предшественников, он не просто принимает известную теорему как истину. Он ее доказывает.

Что значит доказать теорему? Рассказать своего рода математическую историю, где каждый следующий шаг – логическое следствие предыдущих. Каждое очередное утверждение должно быть подкреплено отсылкой к предыдущим и быть выводом из них. Евклид понимал, что этот процесс не может идти вглубь до бесконечности: он должен с чего-то начинаться, и начальное утверждение не требует доказательств: иначе пришлось бы начинать действия с чего-то еще.

Чтобы запустить процесс, Евклид составил несколько основных определений: четких, ясных утверждений для таких основных «технических» понятий, как линия или круг , по сути очевидных. Типичный пример такого определения: тупым называется угол больше прямого.

Эти определения предоставили терминологию, необходимую для формулировки не требующих доказательств утверждений, которые Евклид разделил на два вида: общие утверждения и постулаты . Типичное общее утверждение: объекты, равные одному и тому же, равны и между собой. А типичный постулат: все прямые углы равны между собой.

Мы уже объединили оба эти типа утверждений в один и называем их аксиомами . Математические аксиомы – исходные утверждения, не требующие доказательств. Мы считаем, что аксиомы – как правила игры, и верим, что они всегда выполняются. Мы уже не задаемся вопросом, верны ли эти правила, – мы уже не думаем, что эта игра единственная в своем роде. Всякий, кто собирается участвовать в какой-то конкретной игре, должен соблюдать ее правила; иначе он волен выбрать другую, но в ней правила первой не будут работать.

Правильный многогранник, или платоново тело, – выпуклый многогранник, который состоит из равных граней в виде правильных многоугольников и имеет равное число ребер, выходящих из каждой вершины. Пифагорейцы описывали пять таких правильных многогранников.

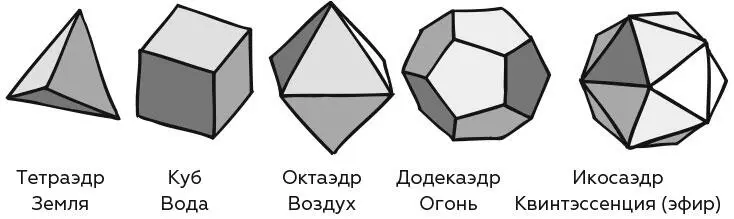
Пять платоновых тел

• Тетраэдр образован четырьмя правильными треугольниками.

• Куб (гексаэдр) образован шестью квадратами.

• Октаэдр образован восемью правильными треугольниками.

• Додекаэдр образован 12 правильными пятиугольниками.

• Икосаэдр образован 20 правильными треугольниками.

Их связывали с четырьмя стихиями Античности: землей, воздухом, огнем и водой – и с пятым элементом – квинтэссенцией.

Во времена Евклида и позже, почти 2000 лет, математикам такое не могло и в голову прийти. Практически все относились к аксиомам как к самоочевидным истинам, чью незыблемость никто не посмел бы оспорить. Евклид недаром приложил все свои таланты, чтобы сделать аксиомы именно такими, – и почти преуспел. Однако одна – аксиома параллельности – оказалась особенно сложной и не такой уж очевидной. Многие ученые пытались вывести ее из более простых общих понятий. Позже мы увидим, к каким поразительным открытиям привели эти попытки.