Мартин Гарднер - Этот правый, левый мир

Вращающиеся цилиндры симметричны, тем не менее, когда два таких цилиндра сближаются торцами, могут возникнуть две существенно различных ситуации. Если в этот момент направления вращения цилиндров (они указаны стрелками) одинаковы, значит сближаются разноименные полюсы. Оба цилиндра начинают сильнее вращаться, и между ними возникает притяжение. Если же при сближении концов направления вращения противоположны, то полюса считаются одноименными. Происходит противодействие во вращении, и цилиндры отталкиваются. Для удобства необходимо повесить на разноименные торцы разные ярлыки. Если мы решили, что написать на одном из концов какого-нибудь цилиндра, то вопрос тем самым автоматически решается для всех остальных цилиндров (то есть всех магнитных полей) во Вселенной. Известно, что ученые решили назвать северным полюсом магнита конец, который притягивается Северным полюсом Земли. Раз такое решение принято, то наименование полюсов любого магнитного поля во Вселенной должно производиться в соответствии с этим выбором.

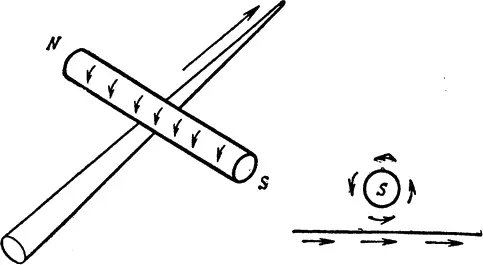
Теперь становится ясным, почему мы не можем воспользоваться опытом с магнитной стрелкой и током (или каким-нибудь аналогичным примером магнитной асимметрии) для передачи на планету X сообщения о правом и левом. Мы можем передать жителям этой планеты, как подвесить магнит над проволокой с током, или объяснить им, что он ведет себя как цилиндр с нарисованными на нем стрелками, который будет поворачиваться так, чтобы стрелки на той стороне цилиндра, которая ближе к току, указывали направление тока (рис. 55). Но дальше мы попадем в безнадежный тупик. Поскольку оба конца цилиндра абсолютно одинаковы во всех отношениях, кроме того, что являются зеркальным отражением друг друга, мы не можем сказать обитателям планеты X , какой конец решено назвать южным, а какой — северным. Мы могли бы сказать: «Северный конец цилиндра тот, с которого видно, что вращение происходит по часовой стрелке». Но что такое «по часовой стрелке»? Магнетизм также не поможет решить проблему Озма, как не помогает в этом случае существование в мире вращающихся колес и цилиндров. То, что Мах, Пастер и их современники приняли за очевидный пример асимметрии в законах природы, оказалось после того, как была создана современная теория магнетизма, псевдоасимметрией.

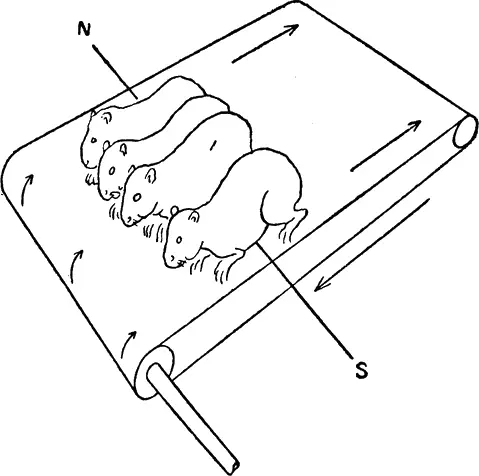
Эксперимент, потрясший Маха, можно смоделировать следующим образом (рис. 56). По движущейся ленте транспортера бегут, выстроившись в ряд, морские свинки. Двигатель вращается так, что верхняя часть ленты движется с юга на север. Это движение соответствует движению электронов в проволоке с юга на север. Морские свинки — это электроны намагниченного железного стерженька. В сторону бежать некуда, повернуть назад трудно, поэтому естественно, что все зверьки бегут в направлении к югу. Правый конец ряда, обращенный на запад, соответствует северному полюсу магнита, а восточный конец ядра — южному полюсу.

Если взять весь ряд и развернуть его северным полюсом на север, то есть повернуть свинок на запад, то этот ряд должен будет повернуть налево, чтобы восстановить первоначальное положение. Направо морские свинки в этом случае никогда не повернут, поскольку им не понравится бежать по движущемуся транспортеру назад. Казалось бы, что можно воспользоваться этим методом для оперативного определения понятий «правый» и «левый». В действительности же этого сделать нельзя, потому что ряд морских свинок обладает билатеральной симметрией. Чтобы разъяснить планете X , который край ряда находится всегда слева, если смотреть навстречу движению ленты, мы должны сперва сказать, где у морской свинки левая, а где правая сторона. А этого-то мы и не умеем делать.

Мах был совершенно прав, когда интуитивно полагал, что магнитное поле симметрично! Потрясающий эксперимент в этом отношении был поставлен лишь в 1957 году, но прежде чем о нем рассказать, читателю придется еще во многом разобраться.

Если бы десять лет назад вы попросили физика найти решение проблемы Озма, то наверняка получили бы ответ: решения не существует. Нет способа, сказал бы ваш собеседник, передать понятия левого и правого мыслящим существам на некоторой планете X без привлечения в качестве примера какой-либо конкретной асимметричной конфигурации, например расположения звезд, луча, поляризованного по кругу света и т. п., которая может наблюдаться и нами и ими. Невозможно предложить эксперимент, использующий любой из известных законов природы, по результатам которого можно было бы операционно определить левое и правое.

Когда в природе что-нибудь остается неизменным, физики любят выражать это постоянство в форме закона сохранения. Например, закон сохранения массы-энергии утверждает, что полное количество массы-энергии в природе постоянно. Масса может переходить в энергию, и наоборот (в соответствии с известной формулой Эйнштейна Е = mc 2), но при этом никогда не происходит увеличения или потери массы-энергии. Закон сохранения четности предполагает неизменность фундаментальной зеркальной симметрии Вселенной, отсутствие предпочтения «правому» или «левому» в основных законах природы.

Понятие «четность» было введено впервые математиками с целью разграничения четных и нечетных чисел. Если два целых числа оба четны или нечетны, то говорят, что они имеют одинаковую четность. Если одно из них четно, а другое нет, то их четности противоположны. Оказалось, что это понятие может быть различным образом применено к любой ситуации, когда предметы явно разделяются на два взаимно исключающих класса, которые могут быть связаны с четными или нечетными числами. Рассмотрим простейший пример. Возьмем три монеты и положим их рядом на столе «орлом» кверху. Будем затем переворачивать монеты по одной в любом порядке независимо от того, какую монету переворачивали перед этим (пусть даже все время одну и ту же монету). Если общее число переворачиваний монет четное , то, каково бы ни было это число — 2, 74 или 3496, мы всегда получим одну из четырех следующих комбинаций:

Опять положим наши монеты «орлом» кверху. Сделаем теперь нечетное число переворачиваний, снова каждый раз выбирая монету независимо от того, какая бралась в предыдущий раз. Можно убедиться, что в итоге всегда получится один из четырех вариантов, изображенных на следующем рисунке (стр. 195).