Макс Тегмарк - Наша математическая вселенная

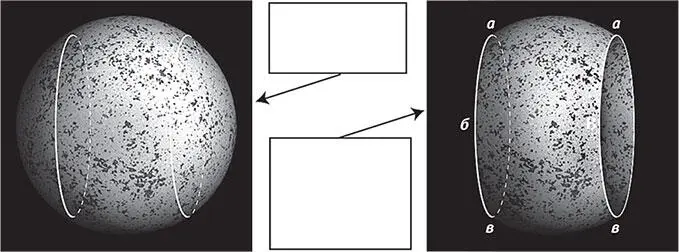
Рис. 6.1.Если в тороидальной вселенной вы пролетите через правую окружность ( справа ), то немедленно окажетесь в соответствующей точке на левой окружности: покинув точку а , вы попадёте в точку а , и т. д. В действительности две точки а являются одной физической точкой. Значит, паттерны космического микроволнового фона вдоль этих двух окружностей должны казаться нам похожими, поскольку в действительности они представляют собой одно и то же.

Но довольно о бесконечном пространстве. Что можно сказать о бесконечном количестве материи? До появления теории инфляции это допущение часто оправдывалось ссылками на принцип Коперника , гласящий, что люди не занимают особенного места в космосе: если галактики есть вокруг нас, значит, галактики должны быть везде.

Что говорят об этом данные последних наблюдений? Например, насколько однородно распределение материи в больших масштабах? В модели островной вселенной , где пространство бесконечно, а вся материя заключена в конечной его области, почти все члены мультиверса I уровня были бы мёртвыми, состоящими лишь из пустого пространства. В прошлом такие модели были популярны. Первоначально островом была Земля и небесные тела, видимые невооружённым глазом, а в начале XX века островом стала известная нам часть галактики Млечный Путь. Модель островной вселенной недавно была окончательно опровергнута наблюдениями. Трёхмерные карты распределения галактик, о которых шла речь в предыдущей главе, показали, что впечатляюще крупномасштабные структуры (группы, скопления, сверхскопления галактик, стены) на больших масштабах уступают место унылой однородности, и никаких целостных структур размером более примерно 1 млрд световых лет не существует.

Чем крупнее структуры мы наблюдаем, тем более однородным кажется заполнение Вселенной материей ( рис. 4.6 ). Если отбросить конспирологические теории, согласно которым Вселенная специально создана так, чтобы нас дурачить, наблюдения недвусмысленно говорят нам: пространство, каким мы его знаем, тянется далеко за границы нашей Вселенной и наполнено галактиками, звёздами и планетами.

Где находятся параллельные вселенные I уровня?

Итак, если параллельные вселенные I уровня существуют, то это просто области пространства размером с нашу Вселенную, которые удалены настолько, что свет от них ещё не успел достичь нас. Но если мы в центре Вселенной, означает ли это, что мы занимаем некое особое место в пространстве? Представьте себе, что вы идёте по большому полю в сильном тумане, которой ограничивает видимость до 50 м, и чувствуете себя так, будто находитесь в центре туманной сферы, за пределами которой, как за краем нашей Вселенной, вам ничего не видно. Но это не означает, что вы в особенном месте, поскольку всякий, кто находится в это время на поле, ощутит себя в центре собственной туманной сферы. Точно так же любой наблюдатель, находящийся в любом месте пространства, обнаружит себя в центре своей вселенной. Кроме того, между соседними вселенными не существует физических границ, как нет особой 50-метровой границы в тумане — поле и туман имеют одинаковые свойства и там, и здесь. Более того, вселенные могут перекрываться, как и туманные сферы. Некто на поле в 30 м от вас может одновременно видеть и вас, и области, которые вам не видны. Так и обитатель галактики в 5 млрд световых лет от нас будет видеть в своей вселенной и Землю, и области космоса, лежащие вне нашей Вселенной.

Если вечная инфляция (или что-либо другое) породила бесконечное число таких параллельных вселенных, насколько далеко находится ближайшая точная копия нашей собственной? Согласно классической физике, Вселенная может быть устроена бесконечным числом способов, так что нет гарантии, что вы когда-либо найдёте идентичную. С классической точки зрения, существует бесконечно много вариантов даже для расстояния между двумя частицами, так что требуется бесконечно много десятичных цифр, чтобы его задать. Однако очевидно, что существует лишь конечное число возможных вселенных, которые человеческая цивилизация смогла бы когда-либо отличить друг от друга: в наших мозгах и компьютерах можно хранить лишь конечное количество информации. Более того, мы можем выполнять измерения лишь с конечной точностью. Современный рекорд точности измерения количественной величины в физике составляет 16 десятичных цифр.

Квантовая механика ограничивает это разнообразие даже на фундаментальном уровне. В следующих двух главах мы узнаем, что квантовая механика вносит в природу внутреннюю размытость, которая лишает смысла разговоры о местоположении объектов с точностью, превосходящей определённый уровень. Вследствие этого ограничения общее число способов, которыми может быть организована наша Вселенная, становится конечным. Согласно консервативной оценке с поправкой в большую сторону, существует не более 10 10 118способов, которыми может быть устроена вселенная размером с нашу. [23]Ещё более консервативное ограничение, известное как голографический принцип, предполагает, что объём размером с нашу Вселенную может быть устроен не более чем 10 10 124способами. [24]В противном случае в него пришлось бы поместить столько вещества, что образовалась бы чёрная дыра, превосходящая его по размерам.

Это огромные числа, больше даже знаменитого гуголплекса. Маленькие мальчики склонны зацикливаться на больших вещах, и однажды я подслушал, как сын с приятелями пытаются обставить друг друга, называя всё большие числа. После триллионов, октиллионов и т. д. кто-нибудь неминуемо сбрасывает G -бомбу — гуголплекс, и на мгновение наступает благоговейная тишина. Гуголплекс — это 1, за которой следует гугол нулей, где гугол — это 1, за которой следует 100 нулей. Так что 10 10 100— это не 1 с 100 нулями, а 1, за которой следует 10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 нулей. Это число настолько велико, что его в принципе нельзя записать: в нём больше цифр, чем есть атомов в нашей Вселенной. (Я всегда подозревал, что «Гугл» — амбициозная компания. Когда я побывал там на конференции, я узнал, что сотрудники называют корпоративный кампус «Гуголплексом».)

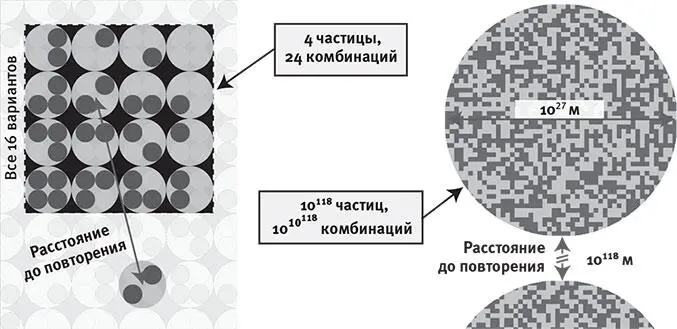
Рис. 6.2.В игрушечной вселенной, где в 4 местах может находиться по одной частице двух типов, существует всего 2 4возможных комбинаций ( вверху слева ). Это означает, что в мультиверсе I типа, состоящем из таких вселенных, в среднем нужно проверить 16 вселенных, чтобы найти повторение одной заданной. Если наша Вселенная подобным же образом содержит 10 118частиц, которые можно скомбинировать 10 10 118различными способами, придётся посетить около 10 10 118параллельных вселенных, прежде чем отыщется идентичная копия.