Макс Тегмарк - Наша математическая вселенная

Критерий № 3 определяет, сколько времени должен осуществляться эксперимент по квантовому суициду на практике, прежде чем непредвиденные события спасут вашу жизнь. Например, каждые несколько лет, примерно раз в 10 8≈ 2 27секунд, в моём районе случается отключение электроэнергии. Значит, если «квантовый пулемёт» работает от электрической сети, а не от собственных батарей, то следует ожидать около 27 щелчков, а затем отключение электричества прервёт эксперимент, поскольку с этого момента будет существовать больше параллельных вселенных с живым мной и неработающим пулемётом, чем с пулемётом действующим. Чем дольше пулемёт проработает, тем больше невероятных событий может реализоваться: например, 36 секунд слыша щелчки, следует ожидать, что пулемёт будет уничтожен метеоритом… В «Автостопом по Галактике» Дугласа Адамса описывается «бесконечно-невероятностный двигатель», который позволяет пережить крайне маловероятные события. Квантовый пулемёт действует именно таким образом.

Особенно интересным я считаю критерий № 1. Допустим, ваше устройство для суицида основано не на квантовой случайности, а на чём-либо вроде подбрасывания монеты. То есть предсказать, выпадет орёл или решка, можно в принципе, но не на практике, поскольку невозможно во всех деталях определить, как первоначально двигалась монета, и выполнить все вычисления. В этом случае, если у вас изначально имелась одна параллельная вселенная, то и после первой секунды она осталась бы, а вот вы оказались бы либо живы, либо мертвы, в зависимости от исходного положения и движения монеты, так что не смогли бы чувствовать себя субъективно бессмертным.

Но что если реален мультиверс I уровня ( гл. 6 )? Тогда вначале должно существовать бесконечно много параллельных вселенных, которые содержат вас в субъективно неразличимых состояниях сознания, но с неизмеримо малыми различиями в начальном положении и скорости монеты. Через секунду вы будете мертвы в половине этих вселенных, но независимо от того, сколько раз эксперимент повторяется, всегда найдутся такие вселенные, где вас никогда не застрелят. Иными словами, описанный жуткий эксперимент может раскрыть существование не только параллельных вселенных III (квантового) уровня, но и параллельных вселенных в более широком смысле.

Знаю, что это может показаться безумием. (В подобных случаях предупреждают: «Не пытайтесь проделать это самостоятельно».) Более того ( гл. 11 ), я теперь не вполне убеждён и в действенности эксперимента с квантовым суицидом, и в реальности квантового бессмертия, поскольку и то, и другое критически зависит от существования в природе бесконечно делимого математического континуума, в чём я сильно сомневаюсь. Но кто знает? Когда наступит роковой день и вы будете уверены, что ваша жизнь подошла к концу, помните: не надо говорить себе, что от вас ничего не останется, поскольку это может оказаться не так. Возможно, вы лично убедитесь, что параллельные вселенные существуют.

Я никак не мог выкинуть из головы мысль: не представляют ли мультиверсы I и III уровней в некотором смысле одно и то же? Можно ли их каким-либо образом объединить, подобно тому, как Максвелл объединил электричество и магнетизм в электромагнетизм, а Эйнштейн объединил пространство и время в пространство-время? С одной стороны, кажется, что их природа различна. Параллельные вселенные I уровня ( гл. 6 ) находятся где-то очень далеко в нашем старом добром трёхмерном пространстве, а параллельные вселенные III уровня из этой главы могут располагаться прямо здесь, в смысле наших трёх измерений, но они отделены от нас в гильбертовом пространстве (абстрактном пространстве с бесконечным числом измерений, в котором обитает волновая функция). С другой стороны, мультиверсы I и III уровней имеют много общего. Жауме Гаррига и Александр Виленкин показали, что параллельные вселенные I уровня, порождённые космологической инфляцией, содержат те же последовательности событий, что и эвереттовские квантовые параллельные вселенные. (Я пришёл к тем же выводам.) Если квантовое событие вызывает два события, происходящих в квантовой суперпозиции ( рис. 8.10 ), фактически расщепляя ваше будущее на две параллельные квантовые ветви, то параллельный квантовый исход, о котором вы сейчас ничего не знаете, происходит также и здесь, в вашей квантовой ветви, но очень далеко в пространстве.

И был ещё один источник беспокойства: Энтони Агирре. Он один из моих лучших друзей, и наши жизни во многом параллельны: мы оба пытаемся найти баланс между карьерой и двумя маленькими сыновьями, оба захвачены глобальными проблемами, вместе основали Институт фундаментальных вопросов ( fqxi.org ), филантропически финансируемую организацию, которая вкладывается в высокорисковые, но обещающие большую отдачу физические исследования, непривлекательные для обычных фондов. Чем же Энтони меня беспокоил? «Что если одни параллельные вселенные равнее других?» — спрашивал он.

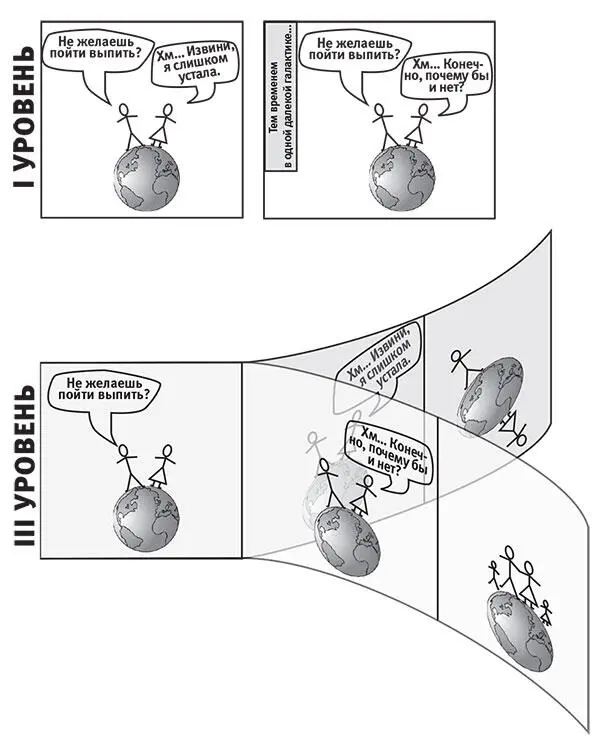
Рис. 8.10.Сравнение параллельных вселенных уровней I и III. В то время как параллельные вселенные I уровня находятся очень далеко в пространстве, вселенные, относящиеся к III уровню, располагаются прямо здесь, возникая за счёт квантовых событий, которые расщепляют классическую реальность на расходящиеся истории. Тем не менее III уровень не добавляет новых историй к имеющимся на уровнях I или II.

Энтони обращал внимание на то, что объяснение квантовых вероятностей, которое я дал в этой главе, отлично подходит, если исходы имеют одинаковую вероятность (как в случае квантовых карт, которые падают лицом вверх или вниз с равными шансами в 50 %), но всё усложняется, если вероятности неодинаковы. Предположим, например, что в начале эксперимента вы чуть наклонили карту, и вероятность (квадрат волновой функции) падения лицом вверх составляет теперь 2/3, а лицом вниз — 1/3. Тогда рис. 8.2 выглядел бы по-прежнему — на нём осталось бы 2 × 2 × 2 × 2 = 16 исходов после четырёх попыток, а наиболее вероятным исходом стало бы падение карты лицом вверх в 50 %, а не в 2/3 случаев. Эверетт спасает положение и всё же умудряется предсказать вероятность 2/3, опираясь на то утверждение, что некоторые исходы имеют большую меру существования, нежели другие (причём её можно вычислить как квадрат волновой функции). Это работает, и многие учёные пытались выстроить тщательно продуманную аргументацию, почему именно квадрат волновой функции должен играть эту роль. Однако Энтони убедил меня в том, что это страшный недостаток в остальном элегантных эвереттовских построений. Меня часто спрашивают, верю ли я в реальность параллельных вселенных Эверетта. Ответ «Да, но… хм… как бы сказать… Некоторые из них реальнее, чем другие» звучит крайне неубедительно.