Макс Тегмарк - Наша математическая вселенная

Знаменитый больной вопрос философии — проблема бесконечного регресса . Например, если мы говорим, что свойства алмаза объясняются свойствами и расположением в нём атомов углерода, свойства атомов углерода — свойствами и расположением в них протонов, нейтронов и электронов, а свойства протонов — свойствами и расположением в них кварков, кажется, что мы обречены вечно пытаться объяснять свойства этих составных частей. Гипотеза математической Вселенной предлагает радикальное решение этой проблемы: на нижнем уровне реальность — это математическая структура, так что её части вообще не имеют внутренних свойств! Иными словами, из гипотезы математической Вселенной вытекает, что мы живём в реляционной реальности , то есть свойства окружающего мира обусловлены не свойствами первичных «строительных блоков», из которых он сложён, а отношениями между «блоками». [68]Внешняя физическая реальность является, таким образом, чем-то большим, нежели суммой её частей. Она может иметь много интересных свойств, хотя её части вообще не имеют собственных свойств.

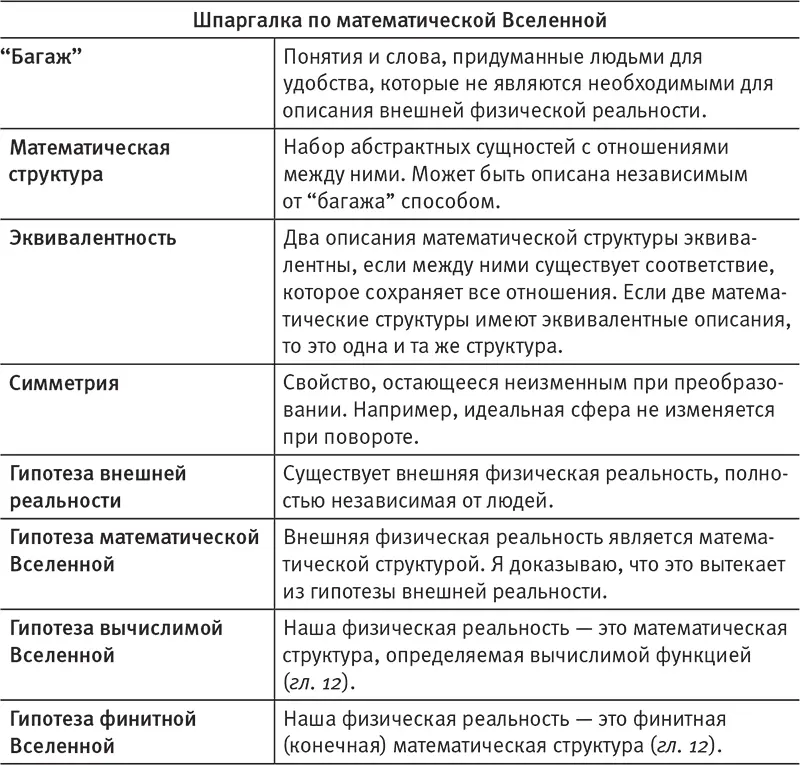
Табл. 10.2.Ключевые понятия, связанные с идеей математической Вселенной.

Математические структуры на рис. 10.7 и 10.8 относятся к семейству математических структур, называемых графами: это абстрактные элементы, часть которых попарно связана. Можно применить другие графы для описания математических структур, соответствующих додекаэдру и прочим платоновым телам на рис. 7.2. Ещё один пример графа — сеть «френдов» в «Фейсбуке». Здесь элементы соответствуют всем пользователям «Фейсбука», и два пользователя связаны, если между ними установлено отношение дружбы. Графы представляют собой лишь одно из множества семейств математических структур. Мы подробнее обсудим математические структуры в гл. 12, а пока разберём ещё несколько примеров.

Есть много математических структур, соответствующих различным типам чисел. Так, натуральные числа (1, 2, 3, …) образуют математическую структуру. Здесь элементами служат числа, и существует много типов отношений. Некоторые отношения (скажем, равно, больше чем, делится на ) могут связывать пары чисел («15 делится на 5»), другие устанавливаются между тремя числами («17 является суммой 12 и 5») и т. д. Постепенно математики открывали более широкие классы чисел, которые образуют собственные математические структуры: целые числа (включающие отрицательные числа), рациональные числа (включающие дроби), вещественные числа (включающие квадратный корень из 2), комплексные числа (включающие квадратный корень из –1) и трансфинитные числа (включающие бесконечные числа). Когда, закрыв глаза, я думаю о числе 5, оно кажется мне жёлтым. Однако во всех этих математических структурах числа сами по себе не имеют свойств, и все их свойства сводятся к их отношениям с иными числами: 5 имеет свойство быть суммой 4 и 1, например, но оно не жёлтое и ни из чего не сделано.

Ещё один обширный класс математических структур соответствует различным пространствам. Например, трёхмерное евклидово пространство, которое мы изучаем в школе, — это математическая структура. Здесь элементами выступают точки трёхмерного пространства и вещественные числа, которые интерпретируются как расстояния и углы. Существует множество других типов отношений. Например, три точки могут удовлетворять тому отношению, что они лежат на одной прямой. Существуют различные математические структуры, соответствующие евклидову пространству с четырьмя и любым другим числом измерений. Математики также открыли множество других типов пространств более общего вида, которые образуют собственные математические структуры, вроде пространства Минковского, римановых, гильбертовых, банаховых и хаусдорфовых пространств. Многие думают, что наше трёхмерное физическое пространство является евклидовым. Однако в гл. 2 мы узнали, Эйнштейн положил этому конец. Сначала его специальная теория относительности показала, что мы живём в пространстве Минковского (включающем время в качестве четвёртого измерения), а затем общая теория относительности заменила пространство Минковского римановым пространством, то есть способным искривляться. Затем появилась квантовая механика ( гл. 7 ), утверждающая, что на самом деле мы обитаем в гильбертовом пространстве. И вновь точки этих пространств ни из чего не сделаны и не имеют цвета, текстуры или каких-либо иных собственных свойств.

Хотя наша коллекция известных математических структур обширна и необычна и ещё больше их пока не открыто, каждую математическую структуру можно проанализировать на предмет симметричности, и у многих обнаруживаются интересные симметрии. Крайне любопытно, что одним из самых важных открытий в физике стало наличие встроенных симметрий и у нашей физической реальности. Так, законы физики обладают вращательной симметрией, то есть во Вселенной нет выделенного направления, которое можно было бы назвать «верхом». Они также, по-видимому, имеют трансляционную симметрию (относительно сдвига), то есть нет особого места, которое можно было бы назвать центром пространства. Многие из упомянутых выше пространств обладают красивыми симметриями, порой совпадающими с наблюдаемыми симметриями физического мира. Например, евклидово пространство обладает как вращательной (нельзя обнаружить различия, если пространство поворачивается), так и трансляционной симметрией (нельзя обнаружить отличия, если пространство сдвигается). У четырёхмерного пространства Минковского ещё больше симметрий, и нельзя обнаружить различий, если выполнен обобщённый поворот между пространственным и временным измерениями (Эйнштейн показал, что именно поэтому кажется, что время замедляется, когда вы движетесь с околосветовой скоростью). В XX веке было открыто множество более тонких симметрий природы. Они лежат в основе эйнштейновских теорий относительности, квантовой механики и Стандартной модели элементарных частиц.

Обратите внимание: свойства симметрии, столь важные для физики, появляются именно благодаря отсутствию собственных свойств у «строительных блоков» реальности, то есть из самой сути того, что значит для неё быть математической структурой. Если выкрасить часть бесцветной сферы в жёлтый, её вращательная симметрия будет нарушена. Подобным образом, если бы точки трёхмерного пространства обладали свойствами, которые делали бы одни точки внутренне отличными от других, пространство утратило бы свою вращательную и трансляционную симметрию. «Меньше — это больше» в том смысле, что чем меньше свойств имеют точки, тем больше симметрий у пространства.