Виталий Сигорский - Математический аппарат инженера

коммутативность

х ∨ y = y ∨ х, х ∧ y = y ∧ х;

ассоциативность

х ∨ ( y ∨ z) = (х ∨ y) ∨ z, х ∧ ( y ∧ z) = (х ∧ y) ∧ z;

дистрибутивность

х ∧ ( y ∨ z) = (х ∧ y) ∧ (х ∨ z), х ∨ ( y ∧ z) = (х ∧ y) ∧ (х ∨ z);

свойство констант

х ∨ 0 = x, х ∧ 1 = x;

свойство отрицания

х ∨ x̅ = 1, х ∧ x̅ = 0.

Приведенные свойства позволяют получить ряд других важных законов и тождеств уже без обращения к таблицам соответствия: 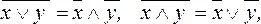(законы де Моргана), х ∨ (х ∧ у) = х ∧ (х ∨ у) = х (законы поглощения) х ∨ х = х ∧ х = х (законы идемпотентности), а также тождества x ∨ (x̅ ∧ y) = x ∨ y; (x ∧ y) ∨ (x ∧ z) ∨ (x ∧ z̅ ); = (x ∧ z) ∨ (y ∧ z̅ ); x̅ = x; 1̅ = 0;

0̅ = 1; x ∨ 1 =1; x ∧ 0 = 0 и т. д.

- 64 -

Так, законы идемпотентности доказываются следующими преобразованиями:

х ∨ х = (х ∨ х) ∧ 1 = (х ∨ х) ∧ (х ∨ x̅ ) = х ∨ (х ∧ (х ∨ х)) = х ∨ 0 = х;

х ∧ х = (х ∧ х) ∨ 0 = (х ∧ х) ∨ (х ∧ x̅ ) = х ∧ (х ∨ x̅ ) = х ∧ 1 = х.

Используя полученные соотношения, имеем:

х ∨ 1 = x ∨ ( x ∨ x̅ ) = (х ∨ х) ∨ x̅ = х ∨ x̅ = 1; x ∧ 0 = x ∧ ( x ∧ x̅ ) = x ∧ x̅ = 0.

Доказательство законов поглощения имеет вид:

x ∨ (x ∧ y) = (x ∧ 1) ∨ (x ∧ y) = x ∧ (1 ∧ y) = x ∧ 1 = x;

x ∧ (x ∨ y) = (x ∨ 0) ∧ (x ∨ y) = x ∨ (y ∧ 0) = x ∨ 0 = x.

Соотношение = х доказывается следующим образом:

из х ∨ x̅ = 1 по закону коммутативности следует x̅ ∨ x = 1, откуда сравнением с 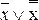= 1 имеем х = .

Интересно доказательство закона де Моргана. На основании свойств отрицания равенство функций x̅ ̅∨̅ ̅y̅ и x̅ ∧ y̅ должно означать, что

(х ∨ у) ∨ ( x̅ ∧ y̅ ) = 1 и (х ∨ у) ∨ ( x̅ ∧ y̅ ) = 0.

Действительно,

(х ∨ у) ∨ ( x̅ ∧ y̅ ) = ((х ∨ у) ∨ x̅ ) ∧ ((х ∨ у) ∨ y̅ ) = (( x ∧ x̅ ) ∨ y ) ∧ (x ∨ (y ∨ y̅ )) =

= (1 ∨ y) ∧ (x ∨ 1) = 1 ∧ 1 = 1, а также

(х ∨ у) ∧ ( x̅ ∧ y̅ ) = (х ∧ ∨ ( x̅ ∧ y̅ ) = (у ∧ ( x̅ ∧ y̅ ) = ((x ∧ x̅ ) ∧ y̅ ) ∨ ((y ∧ y̅ ) ∧ x̅ ) =

= (0 ∧ y̅ ) ∨ ( x̅ ∧ 0) = 0 ∨ 0 = 0.

Следовательно, соотношение x̅ ̅∨̅ ̅y̅ = x̅ ∧ y̅ доказано. Аналогично доказывается и второй закон.

Упрощение записи формул.Операции дизъюнкции и конъюнкции удовлетворяют законам коммутативности и ассоциативности. Поэтому если переменные или формулы связаны только посредством одной из этих операций, то их можно выполнять в лгсбом порядке, а формулы записывать без скобок. Например:

((х 1∨ x 2) ∨ (х 3∨ x 4) ∨ х 5= х 1∨ x 2∨ х 3∨ x 4∨ х 5,

а также (х 1∧ x 2) ∧ (x 3∧ (х 4∧ x 5) = х 1∧ x 2∧ x 3∧ х 4∧ x 5.

Если считать, что операция конъюнкции должна предшествовать операции дизъюнкции (конъюнкция связывает сильнее дизъюнкции), то можно опустить скобки, в которые заключены формулы со знаком конъюнкции. При наличии скобок в первую очередь должны выполняться операции внутри скобок, независимо от их старшинства. Обычно опускают также скобки, в которые заключены формулы со знаком отрицания.

Еще одно упрощение связано с символикой. Знак конъюнкции в формулах можно опустить и вместо х ∧ у писать ху. Операцию конъюнкции часто называют логическим умножением, а операцию дизъюнкции - логическим сложением.

С учетом приведенных условий запись существенно упрощается. Например, формуле (x ∧ (y ∧ z̅ )) ∨ (( x̅ ̅∨̅ ̅y̅ ) ∧ z) соответствует запись xyz̅ ∨ x̅ ̅∨̅ ̅y̅ z.

7. Переключательные схемы.В качестве одной из интерпретаций булевых функций рассмотрим электрическую схему, состоящую из источника напряжения (батареи), лампочки и одного или двух ключей (х 1и x 2). Ключи управляются кнопками с двумя состояниями: кнопка нажата (1) и кнопка отпущена (0). Если в исходном состоянии ключ разомкнут, то при нажатии кнопки он замыкается.

- 65 -

Ключ может быть сконструирован и так, что в исходном состоянии он замкнут, тогда нажатие кнопки означает его размыкание, т. е. приводит к противоположному результату. Поэтому нормально замкнутые ключи обозначим через x̅ 1и x̅ 2.

При соответствующих состояниях кнопок лампочка принимает одно из двух состояний: горит (1) и не горит (0). Состояния кнопок отождествляются со значениями булевых переменных х 1и x 2, а состояние лампочки — со значением функций этих переменных.

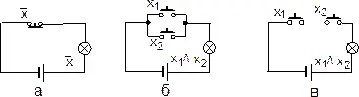
Рис. 22. Переключательные схемы, соответствующие операциям отрицания (а), дизъюнкции (б) и конъюнкции (в)

Операции отрицания соответствует схема с одним нормально замкнутым ключом (рис. 22, а). Если кнопка нажата (х = 1), ключ разомкнут и лампочка не горит, т. е. f(х) = 0; при отпущенной кнопке (х = 0) ключ замкнут и лампочка горит, т. е. f(x) = 1. Операциям дизъюнкции и конъюнкции соответствуют схемы с двумя нормально разомкнутыми ключами (рис. 22, б, в). Легко убедиться, что в схеме рис. 22, б лампочка горит при нажатии хотя бы одной из кнопок, а в схеме рис. 22, в - только при нажатии обеих кнопок одновременно.

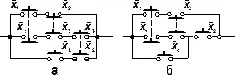
Рис. 23. Переключательная схема, реализующая логическую функцию (а), и упрощенная схема(б).

Любую сложную булеву функцию можно представить некоторой переключательной схемой. На рис. 23,а показана схема, реализующая функцию у = х 1x̅ 2∨ x̅ 1x 2x 3∨ x 3x 4. Та же функция представляется равносильной формулой у = х 1x̅ 2∨ ( x̅ 1x 2∨ x 4)x 3, которой соответствует другая более простая схема (рис. 23, б). Следует иметь в виду, что ключи, обозначенные одинаковыми буквами (х или x̅ ), связаны между собой и управляются общей кнопкой.

В реальных устройствах используются ключи различной конструкции и физической природы (механические, электромагнитные, электронные, гидравлические, пневматические и т. д.) Однако при реализации логических функций многие технические особенности не имеют значения.

- 66 -

Существенными свойствами контактных схем являются исходные положения ключей (нормально разомкнуты или нормально замкнуты) и способ их соединения между собой и внешними устройствами. Эта информация полностью отображается графом, ребра которого соответствуют ключам, а вершины - точкам их соединения. Ребра нормально разомкнутых ключей обозначаются соответствующей переменной (х), а нормально замкнутых - отрицанием переменной (х). Например, контактная схема (рис. 23, б) изображается графом, как показано на рис. 24, а.

При изображении контактных схем графами принимаются некоторые специфические условия и упрощения. Обычно переменные обозначаются в разрывах линий, изображающих ребра.

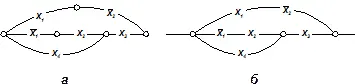
Рис. 24. Граф переключательной схемы (а) и его упрощенное изображение (б).

При этом ребрами считаются только такие линии, которые обозначены какой-либо переменной или ее отрицанием. Другие линии, не являющиеся ребрами графа, могут изображать входы и выходы схемы, связи с другими схемами и т. п. Кроме того, вершины второй степени могут не изображаться, так как им инцидентны пары последовательно соединенных ребер, из которых каждое обозначено соответствующей переменной.