Рафаель Роузен - Математика для гиков
- Название:Математика для гиков
- Автор:
- Жанр:
- Издательство:Литагент АСТ
- Год:2016
- Город:Москва
- ISBN:978-5-17-096852-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Рафаель Роузен - Математика для гиков краткое содержание
После прочтения вы сможете использовать в разговоре такие термины как классификация Дьюи, Числа Фибоначчи, равновесие Нэша, парадокс Монти Холла, теория хаоса, подготовитесь к тексту Тьюринга, узнаете, как фильм получает Оскар, и что это за эффект бразильского ореха.
Математика для гиков - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
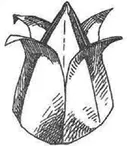
Сам предмет изучения оригами часто является математическим, помимо того что он становится практически независимой математической областью, которая имеет свои аксиомы и доказательства. Некоторые люди создают трехмерные фигуры из модульных компонентов оригами, которые имеют форму треугольников или пятиугольников. Некоторые люди делают оригами-версию платоновых тел, пяти правильных многогранников (это трехмерные фигуры, у которых все грани являются правильными многоугольниками). Другие же создают гиперболические параболоиды, имеющие форму седла и напоминающие нечто среднее между квадратом и бабочкой. И наконец, некоторые используют оригами, чтобы доказать теорему Пифагора.
В некотором смысле оригами и математика, кажется, делят одну ДНК. И нет ничего лучше, чем создавать что-то своими руками, чтобы лучше понять какое-то математическое понятие. Забудьте о карандашах и графиках, попытайтесь найти математику в складывании листов бумаги!
Каждый год в сотрудничестве с организацией OrigamiUSA Американский музей естественной истории создает Праздничное дерево, украшенное фигурками оригами. На елку вешают примерно 800 фигурок. В 2014 году тема основывалась на фильмах «Ночь в музее», поэтому среди фигурок можно было найти Теодора Рузвельта, Тираннозавра Рекса и статую с острова Пасхи.
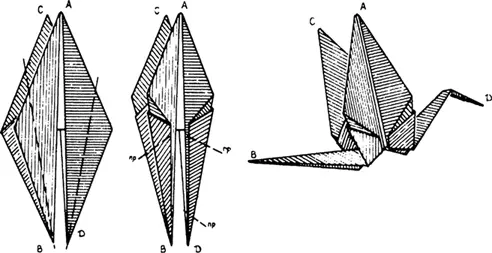
1.11. Математика скрывается за запутанными наушниками
Математическое понятие: теория узлов
Это один из раздражителей современного мира. Вы ищете в кармане или сумке свои наушники и видите, что они спутаны в какой-то невообразимый узел, который невозможно распутать. Вы достаете садовый шланг из подвала – и смотрите-ка – он каким-то образом превратился в узел. Вы достаете из упаковки рождественскую светодиодную гирлянду, которая лежала на чердаке, и обнаруживаете сплошной ком из узлов. Почему так много вещей в нашей жизни постоянно запутываются, несмотря на наши попытки всеми способами избежать этого?

Оказывается, существует математическое объяснение тому, что длинные гибкие вещи, такие, как шнуры, шнурки и веревки, завязываются в узлы. Два физика из Калифорнийского университета в Сан-Диего опубликовали исследование на эту самую тему в 2007 году. По существу, есть только несколько вариантов, при которых скомканные веревкоподобные объекты оставались незапутанными – например, когда секции веревки остаются параллельными самим себе, не касаются друг друга и не имеют точек пересечения – и много-много вариантов, при которых веревка запутывается. Вообще, шнурок или веревка запутываются в течение нескольких секунд. Все, что для этого нужно – это один свободный конец, который пересекает часть самой веревки. На этом этапе свободному концу уже ничего не стоит запутаться в остальной части веревки.
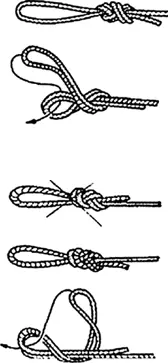
Во время своего исследования команда из Сан-Диего поместила веревки разной длины на 10 секунд во вращающуюся коробку, которая работала от мотора. Они проанализировали получившиеся узлы с помощью математической теории узлов, пытаясь найти математическое уравнение (в этом случае полином Джонса), которое бы соответствовало каждому узлу. (Теория узлов классифицирует узлы по количеству пересечений.) Они обнаружили, что в 96 % случаев узлы были простыми, то есть число пересечений варьировалось от 3 до 11. Команда также обнаружила, что чем короче была веревка – меньше полуметра, – тем меньше узлов на ней образовывалось, но если длина приближалась к 2 или 6 метрам, то вероятность запутывания резко возрастала, вплоть до 50 %. Если же веревка была длиннее, то вероятность сильно не возрастала.
Поэтому вы можете сколько угодно ругать свои наушники, но когда в следующий раз кропотливо будете распутывать их, попытайтесь оценить математику, скрывающуюся за ними.
Запутанные телефонные шнуры породили целую индустрию. В те времена, когда люди полностью полагались на телефонные аппараты с проводом, изобретатели создали специальные устройства против спутывания: от вращающихся на 360 градусов частей до трубок, которые вставлялись в витой шнур, для того чтобы оградить людей от этого ежедневного раздражителя.
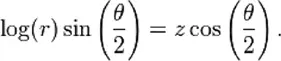
1.12. Почему велосипедные шестерни разных размеров
Математические понятия: геометрия, передаточное отношение
В прошлом велосипеды выглядели чудаковато. В XIX веке у велосипедов были огромные передние колеса и крохотные задние колеса. Педали прикреплялись непосредственно к переднему колесу, которое могло достигать почти 5 футов (более 150 см) в диаметре, а человек должен был запрыгивать на сиденье как на лошадь. Такие велосипеды вскоре вышли из моды, отчасти из-за того, что если велосипед наезжал на кочку, то человек мог запросто перелететь через руль. Позднее производители начали делать велосипеды, используя шестерни и цепи, такое нововведение не только позволило человеку сидеть по центру велосипеда и улучшило тем самым баланс, но также позволило менять передачи в зависимости от местности. Вам необязательно менять передачи, когда вы едете по ровной поверхности, но когда вы поднимаетесь на холм, смена передачи может показать разницу между непринужденной ездой на велосипеде или толканием его в гору. Но как на самом деле работает смена передач? Каким образом они помогают ехать в гору или с горы эффективнее?
Ответ зависит от передаточного отношения. Когда вы подсоединяете шестерню большего размера к шестерне меньшего размера, то если вы проворачиваете одну, то и вторая тоже будет вращаться, но с другой скоростью. Давайте представим, что передняя шестерня в три раза больше, чем задняя. За один оборот передней шестерни задняя будет выполнять три оборота. Подумайте об этом с точки зрения окружности колеса. (Если вы помните уроки математики в школе, длина окружности равна числу Пи, умноженному на диаметр окружности.) Если диаметр передней шестерни равен 3 дюймам, то длина ее окружности равна 3π, то есть примерно 9,42 дюйма. Поэтому если вы поставите точку на крае шестерни, а потом провернете ее один раз, то путь этой точки в пространстве – если перевести его на бумагу – будет равен 9,42 дюйма.
Читать дальшеИнтервал:
Закладка:










