Ханна Фрай - Математика любви. Закономерности, доказательства и поиск идеального решения

Я могла бы написать целую книгу о знакомствах в интернете и о том, что нового они могут рассказать нам о нас самих. К сожалению, придется ограничиться лишь одной главой, но, надеюсь, вы все-таки получите представление о том, как математика помогает в современном, технологичном, поиске любви.

Сайт знакомств – идеальный и простой каталог незнакомцев, готовых вступить в отношения. Начиная работать с этим каталогом, вы можете прежде всего отфильтровать кандидатов по возрасту и месту жительства. Но многие сайты способны на нечто большее: они предлагают пользователям научный подход к поиску пары.

Такие сайты отсеивают варианты, которые не соответствуют вашим требованиям, а также предлагают кандидатуры, которые вы могли бы пропустить, если бы ваши критерии поиска ограничивались только внешностью и местом жительства. Один из самых успешных ресурсов такого рода – OkCupid , бесплатный сайт знакомств, основанный группой математиков и использующий особенно элегантный алгоритм.

Алгоритм – это, в сущности, рецепт: последовательность логических шагов, которые нужно совершить для выполнения той или иной задачи. В данном случае алгоритм OkCupid обрабатывает анкету, которую каждый участник заполняет при регистрации на сайте, в определенной логической последовательности и выводит для каждой потенциальной пары определенную сумму баллов, которая показывает, насколько хорошо партнеры подходят друг другу.

Три ключевых составляющих алгоритма – это: 1) ваши ответы, 2) желательные ответы партнера и 3) степень важности для вас каждого из ответов партнера.

Последняя составляющая особенно важна, потому что позволяет персонализировать процесс. Для кого-то политические взгляды будущего партнера важнее, чем его отношение к детям, а для кого-то – наоборот. Для кого-то обязательное условие – определенный уровень доходов партнера, а для кого-то важно, чтобы он тоже любил фильмы с Райаном Гослингом, хотя в данном случае вы, возможно, не будете настаивать на этом критерии (перечитайте главу 1). В любом случае каждому из нас нужен механизм, позволяющий отфильтровать то, что именно для нас по-настоящему важно.

Спрашивая пользователей, насколько важен для них тот или иной вопрос, OkCupid предлагает им оценить степень важности в баллах по следующей шкале:

1. Совсем не важен – 1.

2. В какой-то степени важен – 10.

3. Достаточно важен – 50.

4. Очень важен – 100.

5. Это обязательное условие – 250.

Таким образом определяется максимальное количество баллов, которое ваш потенциальный партнер может “заработать” в ваших глазах на каждом вопросе.

Чтобы продемонстрировать, каким образом алгоритм рассчитывает степень взаимного соответствия пары, рассмотрим пример, опять же выбрав два совершенно случайных имени: Гарри и Гермиона.

В нашем примере используются всего два вопроса: “Нравится ли тебе квиддич?” и “Умеешь ли ты побеждать темных волшебников?”

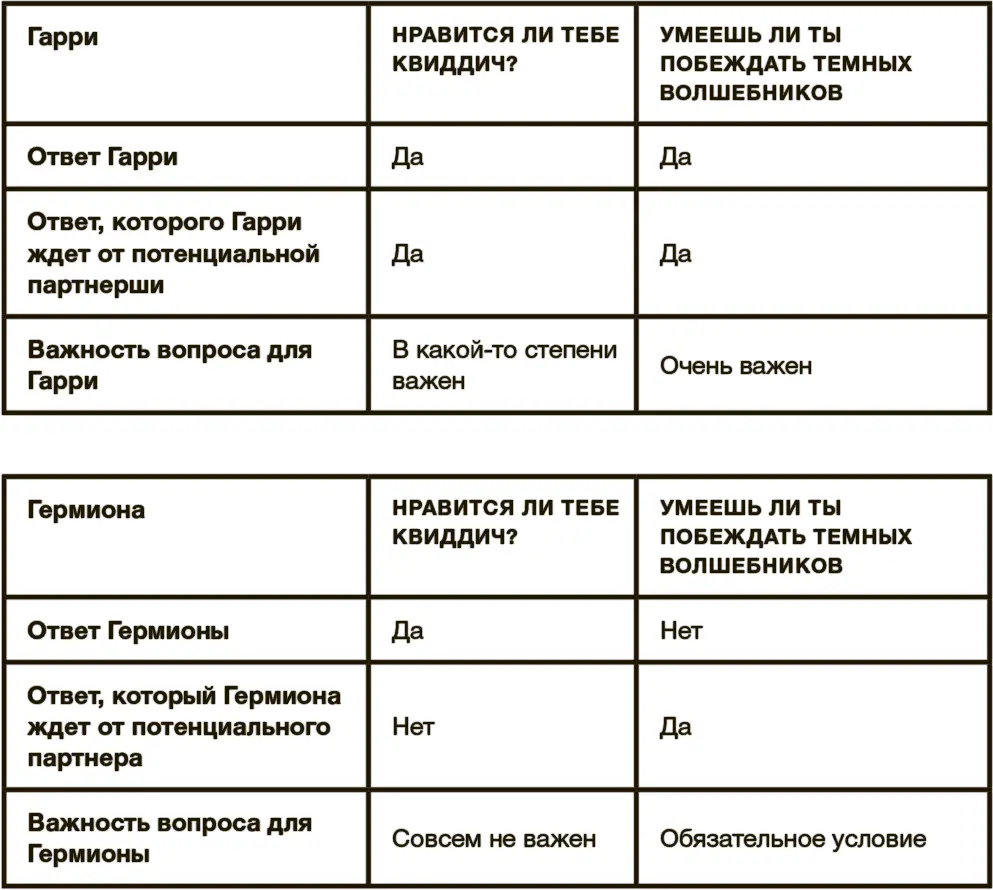
С учетом этих данных поиск ответа на вопрос, подходят ли друг другу Гарри и Гермиона, сводится к трем простым шагам.

Шаг 1

Во-первых, мы должны рассчитать, насколько хорошей парой для Гарри будет Гермиона. Гарри оценил свой первый вопрос лишь как “в какой-то степени важный”, а это означает, что Гермиона может “заработать” на нем максимум 10 баллов. Поскольку она отвечает именно так, как хотелось бы Гарри, то за первый вопрос получает 10 баллов из 10.

Следующий вопрос Гарри оценил как “очень важный”, поэтому Гермиона, ответив на этот вопрос “нет”, не получает ни одного балла. Таким образом, степень ее соответствия ожиданиям Гарри, выраженная в процентах, составляет:

(10+0) ÷ (10+100) = 10 ÷ 110 = 9,09 %.

Шаг 2

Повторяем предыдущий шаг, только на этот раз рассчитываем, насколько Гарри подходит Гермионе. Гермиона оценила первый вопрос всего в один балл (ответ для нее “совсем не важен”). Так как Гарри ответил на вопрос “да” (в то время как Гермиона предпочла бы “нет”), он не получает баллов. Вероятно, Гермиона не хочет, чтобы у ее спутника жизни был один квиддич на уме (и ее можно понять).

Между тем второй вопрос так важен для Гермионы, что он стоит колоссальных 250 баллов. И давайте смотреть правде в глаза – нет человека, на которого не подействовало бы вовремя произнесенное обезоруживающее заклинание “Экспеллиармус”! В результате Гарри зарабатывает эти 250 баллов, и его процент соответствия требованиям Гермионы составляет

(0+250) ÷ (1+250) = 250 ÷ 251 = 99,6 %

Гермиона просто без ума от Гарри!

Шаг 3

Теперь предстоит объединить оба результата, чтобы оценить общее взаимное соответствие. Многие люди при слове “среднее” сразу вспоминают о среднем арифметическом. Способ вычисления последнего еще со школьных лет намертво въелся в нашу память, но для тех, кто все же успел забыть формулу, поясняю: мы складываем показатель Гермионы (99,6 %) с показателем Гарри (округленно 9,1 %), делим сумму на два и получаем 54,35 %, что на 45,25 % отличается от исходных показателей совместимости как для Гарри, так и для Гермионы (только в разные стороны).

Когда речь идет об отношениях, важно мнение обеих сторон. Свидание, которое для одного участника становится самым счастливым моментом в жизни, в то время как второй считает минуты до его окончания, совсем не похоже на свидание, которое обе стороны оценивают как “в целом нормальное”. Тем не менее среднеарифметический показатель в обоих случаях будет равен 54,35 %. Если мы хотим как-то подчеркнуть разницу между этими двумя сценариями, то должны найти другой способ вычисления среднего результата.

В данном случае более целесообразно применять среднее геометрическое, которое основано на умножении, а не на сложении. Для нашего примера, в котором всего два вопроса, формула расчета среднего геометрического [5]будет иметь вид:

(% соответствия Гермионы × % соответствия Гарри)^(½)

или

(99.6 × 9.1)^½ = 30.1 % совместимости.

В среднем геометрическом вместо сложения стоит умножение, что означает, что находится мультипликативная середина: среднее значение должно быть во столько же раз больше меньшего, во сколько большее больше среднего (30,1 % в 3,3 раза больше, чем 9,1 %, и в 3,3 раза меньше, чем 99,6 %). Тем самым мнения обоих участников учитываются более честно. Пусть сам Гарри удовлетворяет всем требованиям Гермионы, но так как его всегда будет раздражать ее неспособность справиться с темными силами, совместимость все равно не превысит 30,1 %.

Вот и все! Обработайте с помощью этого алгоритма сотни доступных вопросов и повторите это для каждого из миллионов пользователей OkCupid – и у вас получится один из самых успешных в мире сайтов знакомств. Подобный алгоритм – один из самых элегантных инструментов изучения личных предпочтений, и неслучайно такие ресурсы, как OkCupid или eHarmony , входят – наряду с Amazon и Netflix – в число самых популярных систем рекомендаций в Сети.