Саймон Сингх - Великая Теорема Ферма

«Премия в 1000 долларов тому, кто первым правильно решит эту головоломку, так и не была никем востребована, хотя тысячи людей утверждали, будто им удалось добиться желаемого. Люди теряли из-за головоломки «15–14» покой и сон. Рассказывали о владельцах лавок, которые забывали открывать свои заведения, о знаменитом священнике, который простоял всю зимнюю ночь под уличным фонарем, пытаясь припомнить, как ему удалось решить задачу. Самое удивительное во всех этих историях о головоломке «15–14» было то, что никто из «решивших» ее не мог вспомнить последовательность ходов, которая привела к победе. Рассказывали, будто лоцманы сажали суда на мели, а машинисты проскакивали без остановки железнодорожные станции. Известный балтиморский издатель рассказывал, как однажды он отправился на ленч и обнаружил, что сотрудники редакции и типографии самозабвенно играют в пятнадцать с полуночи, гоняя по тарелке кусочки пирога».

Рис. 14. Карикатура с изображением мании, порожденной «Игрой в 15» Сэма Лойда (головоломки, в которой все шашки, кроме двух последних, расположены по порядку)

Лойд был абсолютно уверен в том, что ему не придется выплатить объявленную премию в 1000 долларов, поскольку достоверно знал, что невозможно расположить шашки с номерами «14» и «15», не нарушив при этом правильного расположения каких-нибудь других шашек. Так же, как математик может доказать неразрешимость какого-нибудь уравнения, Лойд мог доказать, что предложенная им головоломка не имеет решения.

Доказательство Лойда начиналось с определения величины, которая служила мерой беспорядка в расположении шашек — параметра беспорядка D p . Параметр беспорядка данного расположения шашек равен числу пар шашек, у которых больший номер предшествует меньшему, т. е. номера идут в неправильном, обратном, порядке. Для правильного расположения шашек, как на рис. 15 a, D p = 0.

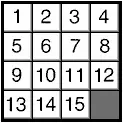
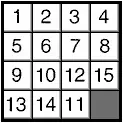
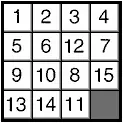
Рис. 15. Передвигая шашки внутри коробочки (но не извлекая их из нее), можно создавать различные неупорядоченные расположения чисел. Для каждого расположения можно количественно измерить беспорядок, вводя параметр беспорядка Dp

Начав с правильного расположения шашек и передвигая их в коробочке (но не вынимая из нее), сравнительно легко получить расположение, представленное на рис. 15 б . В нем шашки идут в правильном порядке до тех пор, пока мы не достигнем шашек 12 и 11. Ясно, что шашка с номером 11 должна предшествовать шашке 12, поэтому шашки в этой паре расположены в обратном порядке. Полный список тех пар, в которых шашки расположены в обратном порядке таков: (12,11), (15,13), (15,14), (15,11), (13,11) и (14,11). Таким образом, при расположении шашек, показанном на рис. 15 б , имеется 6 пар с обратным расположением шашек, и D p = 6. (Заметим, что шашка 10 соседствует с шашкой 12. Это явно неверно, но такое расположение номеров шашек тем не менее не является обратным, поэтому эта пара шашек не вносит вклада в параметр беспорядка.) Еще несколько ходов, и мы приходим к расположению шашек, представленному на рис. 15 в . Составив полный список пар шашек с номерами, идущими в обратном порядке, мы обнаружим, что D p = 12. Важно заметить, что во всех трех случаях а, б и в , значения параметра беспорядка четны (0, 6 и 12). Действительно, если вы начнете с правильного расположения шашек и будете передвигать их, не вынимая из коробочки, то утверждение о четности параметра беспорядка останется в силе. После любого числа ходов, при расположении шашек с пустой клеткой в правом нижнем углу, значение D p всегда будет четным.

Иначе говоря, четное значение параметра беспорядка — свойство всех расположении, получаемых из исходного правильного расположения. В математике свойство, которое сохраняется независимо от того, какие действия производятся над объектом, называется инвариантом.

Но если вы проанализируете расположение шашек в головоломке Лойда «15–14», то обнаружите, что значение параметра беспорядка для нее равно единице: D p = 1, так как только у одной пары с номерами 13 и 15 номера идут в обратном порядке. В головоломке Лойда параметр беспорядка имеет нечетное значение! Но мы знаем, что у любого расположения, полученного из правильного исходного расположения, значение параметра порядка четно. Отсюда следует заключение: расположение шашек в головоломке Лойда «15–14» не может быть получено из правильного исходного расположения, и наоборот, расположение шашек в головоломке Лойда не может быть сведено к правильному расположению. За премию в 1000 долларов Лойд мог быть абсолютно спокоен!

Головоломка Лойда и параметр беспорядка убедительно демонстрируют силу инварианта. Инварианты дают математикам важную стратегию, когда требуется доказать, что один объект невозможно преобразовать в другой. Например, в настоящее время большой интерес вызывает изучение узлов, и специалисты по теории узлов, естественно, пытаются выяснить, можно или нет преобразовать один узел в другой, изгибая и образуя петли, но не разрезая его. Чтобы ответить на этот вопрос, они пытаются найти какое-нибудь свойство исходного узла, которое сохранялось бы при любом изгибании и образовании петель, т. е. инвариант узла. Затем они вычисляют такой же инвариант для второго узла. Если значения инвариантов оказываются различными, то из этого с необходимостью следует вывод о том, что первый узел невозможно преобразовать во второй.

До того, как первые шаги в этом направлении были сделаны Куртом Рейдемейстером в 20-х годах XX века, доказать, что один узел не может быть преобразован в другой, было невозможно. Иначе говоря, до открытия инвариантов узлов было невозможно доказать, что узел «бантиком» невозможно преобразовать в рифовый узел, простой узел или даже простую петлю без какого бы то ни было узла вообще.

Понятие инвариантного свойства занимает центральное место во многих других математических доказательствах, и, как мы увидим в гл. 5, оно сыграло решающую роль в возвращении Великой теоремы Ферма в главное русло развития современной математической мысли.

На стыке XIX и XX веков, благодаря поклонникам Сэма Лойда и его головоломки «15–14», миллионы любителей решать головоломки в Европе и Америке жаждали новых трудных задач. Когда весть о наследстве Вольфскеля дошла до этих начинающих математиков, великая теорема Ферма снова стала самой знаменитой математической проблемой в мире. Великая теорема Ферма была бесконечно более сложной, чем самая трудная из головоломок Лойда, но и приз был несравненно больше.