Дмитрий Кудрец - Построение графиков функций
- Название:Построение графиков функций
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:9785005186119
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Дмитрий Кудрец - Построение графиков функций краткое содержание
Построение графиков функций - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Построение графиков функций
Дмитрий Кудрец
© Дмитрий Кудрец, 2020
ISBN 978-5-0051-8611-9
Создано в интеллектуальной издательской системе Ridero
Построение графиков функций
Существуют различные способы построения графиков функций. Выбор того или иного способа зависит в первую очередь от уровня подготовленности учащегося, пройденного материала, а также непосредственно от условия поставленной задачи.
Рассмотрим основные способы построения графиков функций:
– построение графика функции по точкам;
– построение графика функции с помощью преобразования элементарных функций;
– построение путем сложения, умножения, деления элементарных функций;
– построения графика функции путем исследования функции;
– построение графика функции с помощью производной.
При построении графика следует учесть его вид, т.е. тип функции который описывает тот или иной график. Такие функции называются элементарными или простейшими.
Основными элементарными функциями являются: линейная, степенная, показательная, логарифмическая и тригонометрические функции.
Линейная функция
Линейной называется функция вида f ( x ) = kx + b , где k , b – действительные числа. k называется угловым коэффициентом прямой, он равен тангенсу угла наклона прямой к оси Ох .
Графиком линейной функции является прямая. Для ее построения на координатной плоскости достаточно указать всего две точки.
В зависимости от значений коэффициентов k и b график может принимать различный вид.

Степенная функция
Степенной называется функция вида f ( x ) = x n . В зависимости от значения числа n степенная функция может принимать различный вид.
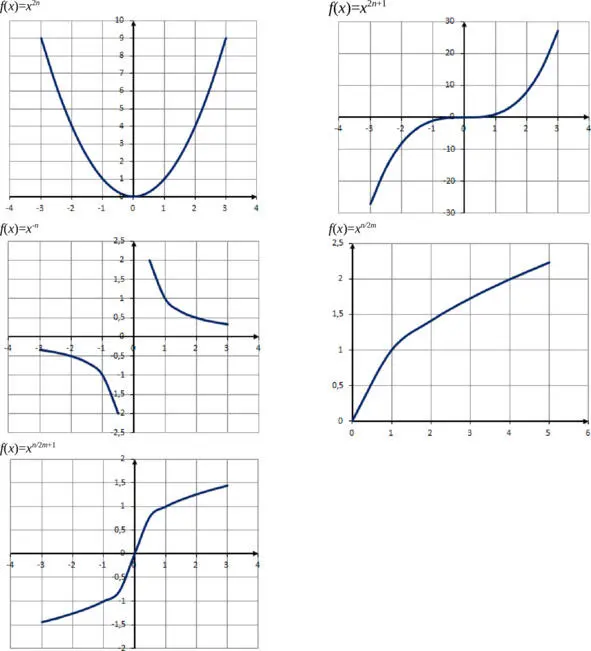
Показательная функция
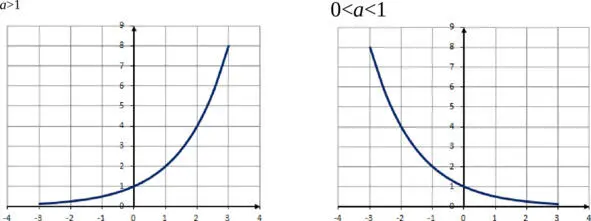
Показательной называется функция вида f ( x) = a x , где a > 0, а≠ 1. График этой функции проходит через точки с координатами (0;1) и (1; а ).
В зависимости от значения числа а , график может иметь вид:
Логарифмическая функция
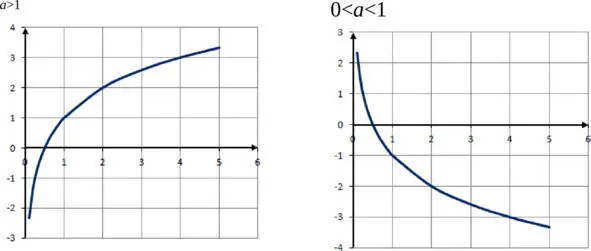
Логарифмической называется функция вида f ( x ) =log ax , где a > 0, а≠ 1.
График логарифмической функции не пересекает ось Оу и проходит через точку с координатой (1; а ).
В зависимости от значения числа а , график логарифмической функции может иметь различный вид.
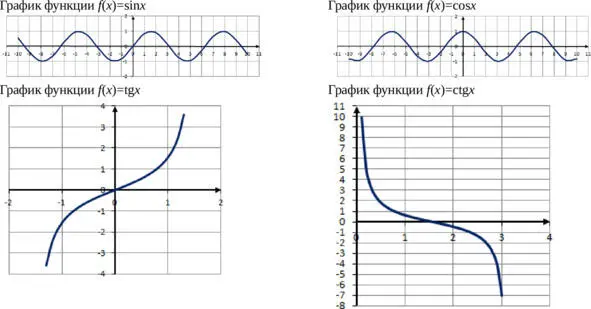
Тригонометрические функции
Тригонометрическими называются функции вида f ( x ) =sin x , f ( x ) =cos x , f ( x ) =tg x , f ( x ) =ctg x .
Построение графика функции по точкам
Построение графика функции по точкам выполняется в следующем порядке:
1. составляется таблица значений аргумента и функции на основе данной формулы;
2. в выбранной системе координат строятся точки, координатами которых являются соответствующие значения переменных, содержащиеся в таблице;
3. полученные точки соединяются плавной линией.
При задании значений аргумента следует учитывать область определения функции.
Пример 1. Построить график функции у = х (6- х ), где -1 < х < 5.
Решение. Функция у = х (6- х ) определена на всем указанном интервале. Составим таблицу значений аргумента и функции:

На координатной плоскости отметим полученные точки и соединим их плавной линией.
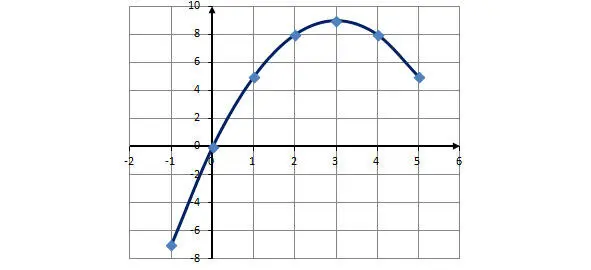
Получим график функции у = х (6- х ) на интервале -1 < х < 5.
При построении графика функции по точкам иногда указывают шаг, т.е. число, через которое выбирается последующее значение аргумента. Чем меньше шаг, тем точнее получается график.
Задание 1.Постойте по точкам график функции…
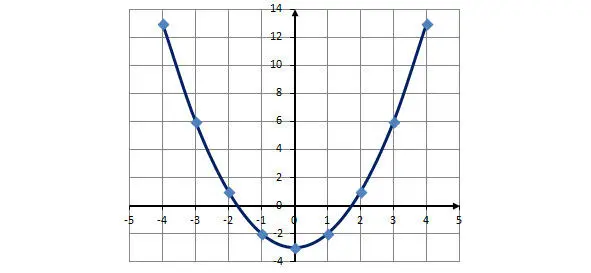
Пример 2. Постройте график функции у = х 2—3, на интервале [– 4; 4] с шагом 1.
Решение. Функция у = х 2—3 определена на всем интервале. Составим таблицу значений. Первое значение аргумента -4. Следующее с учетом шага -4+1=-3 и т. д. пока не получим последнее значение 4.

Отметим точки на координатной плоскости и построим график:
Задание 2.Постройте график функции на заданном интервале с указанным шагом…
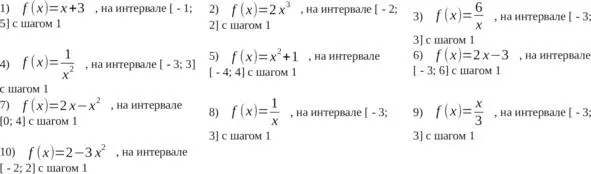
Построение графика с помощью преобразования элементарных функций
Следующим способом построения графиков функций является построение графика с помощью преобразования элементарных функций. Такой способ подходит для построения сложных функций, полученных из элементарных путем параллельного переноса или изменения масштаба.
В этом случае график получается менее точным, но дает более наглядное представление о поведении функции и избавляет от вычислений значений функций.
При построении графиков данным способом можно использовать шаблоны элементарных функций, что значительно упрощает работу.
Построение графика функции - f ( x )
Для построения графика функции - f ( x ) следует график функции f ( x ) симметрично отобразить относительно оси Ох .
Пример 3. Постройте график функции f ( x ) =- x 2.
Читать дальшеИнтервал:
Закладка: