Ингве Фогт - Математические трюки для быстрого счёта
- Название:Математические трюки для быстрого счёта
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:2020
- Город:Москва
- ISBN:978-5-9614-3456-9
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ингве Фогт - Математические трюки для быстрого счёта краткое содержание
Математические трюки для быстрого счёта - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
По-моему, самая важная глава в этой книге – «Чудесный метод счета»: в ней мы учимся тому, чего нам так не хватало, – умножать намного быстрее, чем прежде. А если вы особенно въедливы, загляните в главу под названием «Как комбинировать различные математические фокусы». Да, сочетание различных методов еще сильнее разовьет наше умение быстро считать.
Каждый метод отмечен собственным цветом, так что вы с ходу поймете, какие методы применяются. Не жалейте времени и загляните в разные главы – порядок значения не имеет.
Если вы любите читать книги с конца, то вам представилась отличная возможность. Ознакомьтесь со всеми примерами и проверьте, насколько быстро вы справитесь с заданиями. Вы будете поражены. Порой вам даже станет казаться, будто вы считаете быстрее калькулятора – отчасти потому, что многие случайно набирают на калькуляторе неправильные цифры. Оцените по достоинству каждый метод и проникнитесь осознанием того, что вы – один из немногих, кто теперь на «ты» с этими фокусами. Ну а если захотите вникнуть в суть, загляните в самый конец – там вы найдете доказательства.
2
Проще некуда
Семь правил, которые вам понадобятся
Дорогой читатель, позвольте вас успокоить. Чтобы учиться быстрому счету по этой книге, никаких особых познаний в математике вам не понадобится. Единственное, что от вас потребуется, – это помнить несколько простейших базовых правил, которым учат еще в начальной школе. И больше ничего, обещаю! Честное слово, даже если вы не станете читать эту главу, тех правил достаточно, чтобы вы справился с остальными главами моей книги.
Итак, в основе книги лежат семь легких математических правил. Сравнить их можно с содержимым столярного ящика. Строя прекраснейшие дома, плотник пользуется лишь пилой и топором. Вот и вам понадобится всего несколько математических инструментов, чтобы стать мастером быстрого счета. Некоторые из этих инструментов такие простые, что вы, возможно, сочтете лишним их упоминать. Но я все равно расскажу о них – во-первых, потому что они важные, а во-вторых, потому что они простые и лишний раз порадуют вас.
Правило 1
Первое правило на удивление простое. Порядок чисел при умножении роли не играет:
a × b = b × a
Если буквы вам не по душе, могу продемонстрировать то же самое на простейшем цифровом примере.
3 × 7 даст тот же результат, что 7 × 3. Итак, то, в каком порядке перемножать числа, совершенно не важно.
Правило 2
Второе правило тоже манна небесная для тех, кто пребывает в заблуждении и считает математику сложной.
Порядок чисел при сложении роли не играет.
a + b = b + a
И вот вам пример: 2 + 3 дадут в результате то же число, что и 3 + 2.
Правило 3
Квадрат определенного числа выглядит следующим образом: a × a = a 2.
Обратите внимание на крошечную цифру 2 над последней «а» – читая эту книгу, вы успеете близко с ней познакомиться. Математики называют такие цифры степенями.
Вот еще пример: 3 × 3 можно обозначить как 3 2.
Разумеется, отрицательные числа тоже можно возводить в квадрат:
(‒a) × (‒a) = (‒a) 2= a 2
Например: (‒3) × (‒3) соответствует (‒3) 2.
А вот это невероятно красиво:
(‒3) 2дает тот же результат, что и 3 2.
Правило 4
На квадратные корни тоже приятно посмотреть:
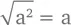
Это означает, что если извлечь квадратный корень из возведенного в квадрат числа, то это же число и получится.
На языке цифр это выглядит вот так:
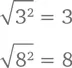
Правило 5
Когда надо умножать отрицательные числа, многие впадают в ступор. Если вас это тоже касается, то быстрому счету вам придется учиться долго.
Одно из важнейших правил звучит так: минус на минус дает плюс.
(‒x) × (‒y) = x × y
Примеры:
(‒2) × (‒3) = 2 × 3 = 6
(‒4) × (‒5) = 4 × 5 = 20
А вот если минус умножить на плюс, то получится, наоборот, минус:
(‒x) × y = ‒(x × y)
Примеры:
(‒2) × 3 = ‒(2 × 3) = ‒6
4 × (‒5) = ‒(4 × 5) = ‒20
Запомним это – минус на минус и минус на плюс, и тогда все минусы математики превратятся для вас в плюсы!
Правило 6
Если хотите понять доказательства приведенных в этой книге методов, придется научиться разлагать числовые выражения на множители и раскрывать скобки:
a(b + c) = ab + ac
(a + c)(b + d) = ab + ad + cb + cd
Вот и все – больше про разложение на множители знать нам ничего не понадобится.
Правило 7
Некоторые методы быстрого счета в этой книге основаны на трех видах квадратичных тождеств, которые включены в стандартную школьную программу. Все они – особые случаи правила 6:
(a + c)(b + d) = ab + ad + cb + cd
Квадратичное тождество первого типа:
(a + b) 2= a 2+ 2ab + b 2
Квадратичное тождество второго типа:
(a ‒ b) 2= a 2‒ 2ab + b 2
Квадратичное тождество третьего типа:
(a + b)(a ‒ b) = a 2‒ b 2
С этими семью правилами в готовальне у вас есть все шансы стать чемпионами быстрого счета. Ну что ж, пора отправляться завоевывать мир! Удачи и успехов!
3
Ходячий калькулятор
Чемпион мира по быстрому счету
В начальной школе я терпеть не мог спорт, зато мечтал стать чемпионом мира по решению в уме всяких математических примеров. Поэтому мне казалось ужасно несправедливым, что школьные спортсмены то и дело выступали на разных соревнованиях, ведь соревнований по математике просто не существовало. Сейчас-то я понимаю, что мое мнение о собственных математических способностях было необоснованно завышенным, я жил в мечтах: хотя считал я и правда довольно быстро, а числа так просто обожал, моих способностей не хватало, если числа в примерах были больше приведенных в таблице умножения. Впрочем, об этом никто не догадывался. Слухи о моих феноменальных математических способностях разлетались со скоростью света и с действительностью ничего общего не имели. Никогда не забуду, как мама одного из моих одноклассников на глазах у всего класса погладила меня по голове и выразила свое восхищение: еще бы, ведь я умею в уме перемножать многозначные числа. Мне тогда было девять лет. А еще мама моего одноклассника слышала, будто я умею и миллионы перемножать. Все это было неправдой, но стеснительность помешала мне опровергнуть слухи. Я смотрел на эту женщину и вспоминал, как однажды, будучи первоклашкой, возвращался из школы домой и был пойман шестиклассниками, которые потребовали сделать за них домашку по математике. Они крепко держали меня (впрочем, особых усилий от них не требовалось – я был самым мелким во всей школе) и, пока я не решил все задачки, не отпускали.
Задачки у них оказались очень простыми. В одной я нарочно допустил ошибку – хотел проверить, заметят ли они, но они, к моей великой радости, ничего не заподозрили. Легенда о моем таланте вдребезги разлетелась в шестом классе, когда отец отвел меня к университетскому профессору, предварительно рассказав ему о моих невероятных успехах. Профессор дал мне несколько примеров и выглядел довольно-таки разочарованным, когда я ошибся в первом же из них. Именно в тот момент я понял, что лучше всего считаю в спокойной обстановке и наилучшее впечатление произвожу на тех, кто сам с математикой не дружит.
Читать дальшеИнтервал:
Закладка: