Яков Перельман - Живой учебник геометрии

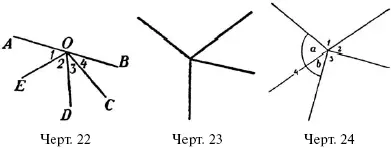
Подобным же образом можно найти, чему равна сумма углов,! расположенных вокруг общей вершины, как на черт. 23. Продолжив одну из сторон за общую вершину (черт. 24), получим две группы углов: группу 1 и а, сумма которых равна двум прямым (почему?), и группу углов 2, 3, Ь, сумма которых равна также двум прямым углам; значит, сумма всех углов вокруг общей вершины равна 4 прямым углам.

Повторительные вопросы

Чему равна сумма смежных углов? – Сумма нескольких углов, расположенных по одну сторону прямой линии? – Сумма всех углов, расположенных вокруг общей вершины?

Предварительные упражнения

1) На черт. 25 уг. 1 = 48°. Найти прочие углы.

2) На черт. 25 уг. b = 136 °. Найти прочие углы.

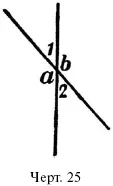
Когда две прямые линии пересекают друг друга (черт. 25), они образуют две пары углов, стороны которых составляют продолжение одни других: одна пара – уг. 1 и уг. 2; другая – уг. а и уг. b. Особенность противоположных углов та, что углы, составляющие такую пару, всегда равны между собою: у г. 1 = уг. 2, уг. а = у г. b. Действительно, если например (черт. 25) уг. 1 = 40°, то уг. b = 180° – 40° = 140°, уг. 2 = 180° – 140° = 40°, и уг. а = 180° – 40° = 140°; мы видим, что уг. 1 = уг. 2, и уг. а = уг. b. Вообще, так как уг. 1 вместе с углом а равен двум прямым (почему?), а уг. 2 вместе с тем же углом а тоже равен двум прямым, то ясно, что уг. 1 должен равняться уг. 2. Итак:

П р о т и в о п о л о ж н ы е у г л ы р а в н ы.

Повторительные вопросы.

Какие углы называются противоположными? знаете свойство противоположных углов?

До сих пор мы говорили только о прямых линиях. Из к р и в ы х линий остановимся на о к р у ж н о с т и (черт. 26). Окружность чертят циркулем. Острие ножки раздвинутого циркуля втыкают в бумагу, другую же ножку с карандашом вращают вокруг первой; когда карандаш сделает полный оборот, он проведет на бумаге замкнутую кривую – окружность. Та точка, в которую было воткнуто острие циркуля, называется ц е н т р о м окружности. Понятно, что все точки окружности удалены от центра на одинаковое расстояние; это расстояние называется р а д и у с о м окружности. Значит:

О к р у ж н о с т ь е с т ь к р и в а я л и н и я, в с е т о ч к и к о т о р о й о д и н а к о в о у д а л е н ы о т о д н о й

т о ч к и, н а з ы в а е м о й ц е н т р о м.

Прямая, соединяющая две точки окружности через центр, называется д и а м е т р о м.

Всякая часть окружности называется ее д у г о ю (черт. 27).

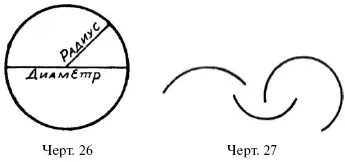
Плоская фигура, ограниченная окружностью, называется к р у г о м.

Повторительные вопросы

Что такое окружность? Центр? Радиус? Дуга? – Покажите все это на чертеже. – Все ли радиусы одной окружности равны между собою? – Что больше: диаметр или радиус? Во сколько раз?

Применения

3. Гудок завода слышен на 4 км. Начертить в масштабе 1 км в 1 см границу местности, где слышен гудок этого завода.

Р е ш е н и е. Вокруг точки, обозначающей положение завода, начертить окружность радиусом 4 см.

4. Радиус круга 100 см. Некоторая точка удалена от центра на 40 см. Лежит ли она внутри круга или вне его? Каково ближайшее расстояние от этой точки до окружности?

Р е ш е н и е. Точка лежит внутри круга. Ближайшее расстояние ее от окружности надо считать вдоль диаметра, проведенного через эту точку; оно равно 60 см. Дальнейшее расстояние (вдоль того же диаметра) – 140 см.

Две прямые линии могут пересечься друг с другом только в одной точке; более одной общей точки две разные прямые иметь не могут, – иначе они сливаются одна с другой. В скольких же точках могут пересекаться друг с другом прямая и окружность?

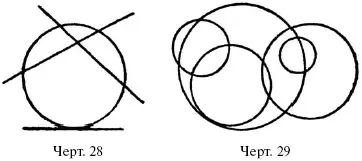
Начертите одну или несколько окружностей и пересеките их прямыми линиями (черт. 28). Вы убедитесь, что прямая и окружность могут встречаться или в двух точках или в одной. Более двух общих точек прямая и окружность иметь не могут.

Подобным же испытанием мы найдем, что и две окружности не могут иметь более двух общих точек: они встречаются или в одной или в двух общих точках (черт. 29). Итак, запомним:

П р я м а я и о к р у ж н о с т ь и л и д в е о к р у ж н о с т и н е м о г у т и м е т ь б о л е е д в у х о б щ и х т о ч е к.

Применения

5. В городе два завода в 8 км друг от друга. Гудок одного слышен на 5 км, другого – на 6 км. Изобразите, в выбранном вами масштабе, границы местности, где слышны гудки обоих заводов.

Р е ш е н и е. Выберем масштаб 2 км в 1 см. Взаимное удаление заводов изобразится тогда отрезком в 4 см. Наметив на чертеже две точки в расстоянии 4 см одна от другой, проведем вокруг одной из них (как около центра) окружность радиусом 21/2 см, а вокруг другой – радиусом 3 см. Окружности пересекутся, и общая часть обоих кругов будет изображать местность, где слышны гудки обоих заводов.

6. Две радиостанции расположены в 600 км одна от другой. Дальность приема одной 400 км, другой – 300 км. Начертите, в масштабе 100 км в 1 см, границу местности, где можно принимать обе станции.

Р е ш е н и е сходно с решением предыдущей задачи

Какою мерою измеряются углы? Д л и н у линий измеряют д л и н о ю определенной линейки (метром); в е с вещей – в е с о м определенной гири. Так и у г л ы измеряют определенным у г л о м, который принимают за меру углов. Мерою для углов избран

п р я м о й угол, потому что все прямые углы имеют одну и туже величину. Но прямой угол слишком велик, чтобы служить удобной единицей меры; поэтому пользуются некоторою д о л е ю его – именно 90-й. Прямой угол делят на 90 равных частей, и такими частями измеряют все прочие углы, т. е. узнают, сколько этих частей заключается в измеряемом угле. 90-я доля прямого угла называется у г л о в ы м г р а д у с о м. Угол в один градус весьма мал; все же для точных измерений приходится пользоваться даже долями такого угла. Принято употреблять для этого 60-ю долю градуса; она называется у г л о в о ю м и н у т о ю. Итак:

прямой угол = 90 углов, градусам,

градус = 60 углов, минутам.

На письме градус сокращенно обозначается маленьким кружком (как и градус температуры), а минута – знаком ’. Например, 23° 27’ означает 23 градуса 27 минут.

Объясним теперь, каким образом производится измерение углов на практике.