Эмилия Александрова - Искатели необычайных автографов

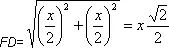
— Отлично, — сказал Мате. — Стало быть,

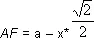
Теперь все стороны треугольника AKF выражены у нас через искомое число х: KF = х, АК = a-x, и, наконец,

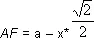
Снова обратимся к теореме Пифагора и получим, что KF 2 = АК 2+ AF 2, то есть

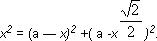
— Что-то вроде квадратного уравнения, — сообразил Фило.

— Вот-вот. Надо лишь привести его в приличный вид.

Мате раскрыл скобки и перенес все члены уравнения в левую часть равенства:

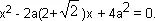
— Решив уравнение по обычной формуле, — продолжал он, — получим:

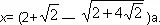
— Э, нет, — заартачился Фило, — перед большим корнем полагаются два знака: плюс и минус. А вы написали только минус…

— Замечание верное, но ведь мы с вами не отвлеченное квадратное уравнение решаем, а ищем вполне конкретную сторону пятиугольника. А она, если вдуматься, никак не может быть больше стороны квадрата. Так что на сей раз хватит с вас и одного минуса.

— Невелика выгода. Ответ у вас все равно некрасивый: корень на корне и корнем погоняет.

Мате засмеялся. Этот Фило определенно делает успехи! Одной правильности ему уже мало. Что ж, придется предложить ответ поизящнее. Такой, например: если принять, что корень из двух приближенно равен 1,41, то икс — также приближенно — равен 0,65 а.

— Совсем другое дело? — сказал Фило. — Но там, между прочим, были еще две геометрические задачи.

— Благодарю за напоминание. Только теперь ваша очередь решать.

Фило обомлел. Как? От него требуют, чтобы он решал задачу один? Самостоятельно?

— Вот именно, — непреклонно подтвердил Мате. — Единственное, что я могу для вас сделать, это напомнить, в свою очередь, условия задач. Итак, слушайте. Задача вторая. В равносторонний треугольник надо вписать квадрат, одна сторона которого лежит на основании треугольника. Произвести это следует так, чтобы квадрат вместе с образовавшимся над ним малым треугольником составлял равносторонний пятиугольник.

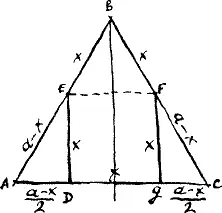
Фило мрачно вздохнул и задумался. Через некоторое время, однако, лицо его прояснилось. Он взял у Мате блокнот, вычертил равносторонний треугольник АВС и вписал в него квадрат DEFg.

— Само собой разумеется, что квадрат пока что приблизительный, так же как и равносторонний пятиугольник DEBFg.

— Ну, ну, — подбадривал Мате, — дальше…

— Дальше обозначим стороны большого треугольника через a , а стороны пятиугольника через х и рассмотрим прямоугольный треугольник AED. Гипотенуза его АЕ = а — х. Катет ED = х, а катет AD = (a — x)/2. Так ведь?

— Клянусь решетом Эратосфена, так!

— Тогда остается применить теорему Пифагора:

АЕ 2= ED 2+ AD 2.

А уж отсюда получим выражение:

(а — x) 2= x 2+ ((a — x)/2) 2.

После этого Фило запнулся и посмотрел на Мате так жалобно, что сердце у того не выдержало, и вскоре перед ними красовалось следующее квадратное уравнение:

x 2+ 6ах — 3a 2 = 0

Решив его, они определили, что

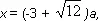
и откинулись от стола, весьма удовлетворенные своей деятельностью.

— Ну, — ехидно полюбопытствовал Мате, — что же вы не спросите, почему перед корнем вместо двух знаков только один?

Фило гордо подбоченился: стоит ли спрашивать о том, что и так ясно? Ведь сторона квадрата не может быть отрицательной! Стало быть, минус ни при чем.

Далее он относительно быстро подсчитал, что

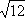
приближенно равен 3,46, а раз так, значит, х ≈ (-3 + 3,46)а = 0,46а.

— Всё! Переходим к третьей задаче.

— Надо ли? — усомнился Мате. — Думаю, вы отлично справитесь с ней дома.

И он протянул товарищу листок, на котором было написано: «в равнобедренный треугольник с основанием 12 и боковыми сторонами 10 вписать равносторонний пятиугольник, один из углов которого — угол при вершине, а одна из сторон лежит на основании треугольника».

— Скряга! — укорил его Фило.

— Ничего, учитесь мыслить самостоятельно! Ну же, не капризничайте… Хотите, объясню вам принцип счета шестидесятеричной системы счисления?

«Нечего сказать, утешил!» — подумал Фило.

— А вы уверены, что я в состоянии это понять? — спросил он довольно кисло.

Мате скорчил гримасу, означающую: «На глупые вопросы не отвечаю», — и приступил к объяснениям.

— Для сравнения возьмем какое-нибудь число, записанное в нашей, десятичной, системе, ну хоть 2324. В этом числе каждый последующий разряд, начиная справа, больше предыдущего в десять раз. Значит, число это можно записать так:

2 х 1000 + 3 х 100 + 2 х 10 + 4 х 1,

а это не что иное, как:

2 х 10 3+ 3 х 10 2+ 2 х 10 1+ 4 х 10 0

В шестидесятеричной системе каждый последующий разряд больше предыдущего не в 10, а в 60 раз. Поэтому та же запись 2324 расшифровывается уже по-другому:

2 х 60 3+ 3 х 60 3+ 2 х 60 1+ 4 х 60 0.

А это, — Мате сосредоточенно пошевелил губами, — это составляет 442 924. Добавлю, что цифры в шестидесятеричной системе счисления пишутся на некотором расстоянии друг от друга. Вот, собственно, и всё. Ну как, постижимо?

— Пока — вполне, но в ответе на алгебраическую задачу у мессера Леонардо были еще какие-то значки…

— Не значки, а римские цифры. Так в шестидесятеричной системе записывают дробные числа. Опять-таки для сравнения возьмем какую-нибудь десятичную дробь. Например: 2,135. Что это такое? Это

2/10 0+ 1/10 1+ 3/10 2+ 5/10 3

В шестидесятеричной системе место знаменателя 10, естественно, займет другой: 60. Стало быть, если в ответе на алгебраическую задачу у мессера Леонардо было записано

1 022 I7 II42 III33 IV4 V40 VI,

то читать это следует так:

1/60 0+ 22/60 1+ 7/60 2+ 42/60 3+ 33/60 4+ 4/60 5+ 40/60 6

Подсчитайте — и ответ Фибоначчи в десятичном счислении перед вами!

Фило испуганно отшатнулся:

— Вы что? Да я же до утра не кончу!

— Ладно, ладно, — примирительно проворчал Мате, — все уже давно подсчитано. Икс у Леонардо приближенно равен

1,368808107853.

Фило был потрясен. Вычислить иррациональный корень с таким невероятным приближением, да еще в шестидесятеричной системе!

Мате усмехнулся:

— Есть у Фибоначчи вещи и более удивительные…

— Что вы имеете в виду?

Но Мате, которому всегда нравилось разжигать любопытство приятеля, пропустил вопрос мимо ушей.