Эмилия Александрова - Искатели необычайных автографов

— По известной формуле, — сейчас же соображает Асмодей. — Квадрат расстояния между двумя точками равен сумме квадратов разностей координат этих точек, иначе говоря

d 2 = (X 1— Х 2) 2+ (У 1— У 2) 2.

— Очень хорошо. Подставим в эту формулу координаты соответствующих вершин треугольника. Тогда:

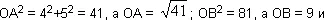
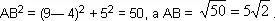
Ну, а теперь построим на сторонах нашего треугольника новые треугольники, на сей раз равносторонние. Намечаю их пунктиром. Буквами n, m и р обозначим точки пересечения медиан в каждом из них. Это и будут их центры тяжести. Точки эти, как известно, находятся на расстоянии двух третей медианы, считая от вершины. В первом равностороннем треугольнике это Am = От. Во втором — An = Вn. В третьем — Вр = Ор. Но так как в равностороннем треугольнике медианы являются в то же время и высотами, а высота в этом случае равна половине стороны, умноженной на

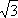
то

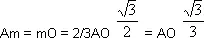
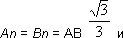
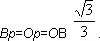
Иначе:

(Ат) 2= (mO) 2 = (AO) 2 /3 = 41/3, (An) 2= (Вn) 2= AB 2/3 = 50/3;

(Вр) 2= (Ор) 2= OB 2/3 = 27.

Мате на мгновение отрывается от чертежа и, убедившись, что Фило еще жив, продолжает:

— Далее обозначим искомые координаты центров тяжести равносторонних треугольников. Точки m: х 1, у 1; точки n: x 2 , у 2; точки р: х 3, у 3. Займемся сперва одним треугольником и по известной уже нам формуле о квадрате расстояния между двумя точками вычислим, что

(Am) 2= (Оm) 2= (x 1— 4) 2+ (y 1— 5) 2= x 1 2+ y 1 2= 41/3.

Решая систему двух уравнений:

(x 1— 4) 2+ (y 1— 5) 2= x 1 2 + y 1 2и x 1 2+ y 1 2= 41/3, найдем, что

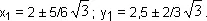
— А как это у вас получилось? — неожиданно для себя самого интересуется Фило.

— По-моему, это понятно всякому школьнику, — сердито отвечает Мате.

— Допустим. А как же быть с двумя знаками перед вторыми слагаемыми? Какой из них выбрать?

— Ну, а это уж где как. Обратите внимание на то, что первые слагаемые (2 и 2,5) — это координаты середины стороны ОА. В самом деле:

(O + 4)/2 = 2 и (O + 5)/2 = 2,5

А точка т лежит слева от этой середины, но выше ее. Следовательно, в первом равенстве (x 1) надо сохранить знак минус, а во втором (у 1) — знак плюс. Поэтому окончательно:

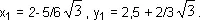
Точно таким же образом найдем координаты точек n и р:

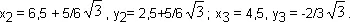
Остается вычислить расстояния между т и п, п и р, р и т. Обозначим их буквой dс соответствующими индексами: тп, пр и рт. Тогда:

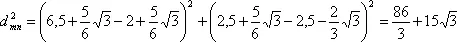
Если теперь вычислить

окажется, что все три результата одинаковы:

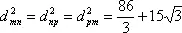
Ну, а раз равны квадраты расстояний, то равны и сами расстояния. Стало быть, соединив точки m, n и р, мы получим равносторонний треугольник.

— Квод демонстрандум эрат! Что и требовалось доказать, — торжественно заключает Асмодей.

— Не забудьте рассмотреть еще два частных случая первоначального треугольника, — суетливо напоминает Мате. — Когда сумма двух сторон равна третьей и когда одна из сторон равна нулю. — Он протягивает Фило и Асмодею заранее заготовленные чертежики. — Как видите, моя теорема справедлива также и для них.

— Благодарю вас, мсье! Поверьте, мне было чрезвычайно интересно! Поздравляю с удачей! — рассыпается бес, но вдруг совершенно неожиданно зевает и страшно смущается. — Пардон, мсье! Не подумайте, что это от вашей теоремы. Всему виной чай. Он всегда действует на меня, как снотворное. С вашего разрешения я вздремну немножко…

Он взлетает на верхнюю полку и скрывается в книге Лесажа, с силой захлопнув за собой картонную обложку. В ту же минуту оттуда начинает исходить легкое блаженное похрапывание: «Хрр-фью… хрр-фью…»

Филоматики растроганно переглядываются.

— Перерыв?

— Перерыв!

— Открываем наше вечернее заседание, — объявляет Фило, когда все они снова сидят за столом и Асмодей кулачком протирает заспанные глаза. — Что у нас на повестке… пардон, на чашке дня?

Бес молча указывает на рисунок, где три блистательных кавалера и одна изысканная дама играют в карты.

— Эпизод под названием «В великосветском салоне», — определяет Фило.

Все еще позевывая, Асмодей заглавие одобряет, считает, однако, необходимым добавить, что к этому эпизоду примыкает еще один: «Встреча на улице Сен-Мишель», связанный с ним общей темой «Теория вероятностей». Кроме того, прежде чем перейти к обсуждению, не мешает установить дату…

Мате уверенно объявляет, что разговор за карточным столом мог быть только зимой 1654 года.

— Почем вы знаете? — любопытствует Фило.

— Да потому что речь, если помните, шла о переезде Паскаля и герцога Роанне в Пор-Рояль. Отсюда следует, что интересующий нас эпизод происходил уже после обращения Паскаля, которое, как я выяснил, относится к 23 ноября 1654 года. И судя по тому, что маркиза об этом узнать не успела, разговор ее с де Мере отстоит не слишком далеко от указанной даты. Он мог состояться в конце ноября или в начале декабря.

— Мог-то мог, но вот состоялся ли? — неосторожно прорывается у Фило.

— Пф! — Асмодей возмущенно фыркает и просыпается окончательно. — Не все ли равно! Важно другое: убедительно или неубедительно? Вероятно или невероятно?

— Вероятно, вероятно! — дружно успокаивают его филоматики.

— Вот и перейдем к задачам о вероятностях, о которых так красноречиво рассказывал шевалье де Мере, — ловко поворачивает разговор черт. — Начнем, как полагается, с начала, то есть с первой задачи. Суть ее такова: двое играют в кости, бросая по два кубика сразу. Первый ставит на то, что хотя бы один раз выпадут две шестерки одновременно. Другой — на то, что две шестерки одновременно не выпадут ни разу. Спрашивается, сколько надо сделать бросков, чтобы шансы на выигрыш первого игрока превысили шансы второго.