Даглас Хофштадтер - ГЕДЕЛЬ, ЭШЕР, БАХ: эта бесконечная гирлянда

Черепаха : Кстати о суммах — это мне напомнило теорию чисел. Там тоже бывает возможно разложить теорему на составляющие ее символы, расположить их в новом порядке и получить новую теорему.

Муравьед : Никогда об этом не слышал; хотя должен признаться, что в этой области я полнейший невежда.

Ахилл : Я тоже в первый раз слышу — а ведь я прекрасно осведомлен в этой области, хотя и не должен сам себя хвалить. Думаю, что г-жа Ч готовит один из своих сложных розыгрышей — я ее уже хорошо изучил.

Муравьед : Кстати о теории чисел — это мне напомнило опять об И. С. Ф. Как раз в этой области он прекрасно разбирался. Теория чисел обязана ему несколькими важными открытиями. А Мура Вейник, наоборот, удивительно несообразительна, когда речь заходит о чем-то, имеющем даже отдаленнейшее отношение к математике. К тому же, у нее довольно банальные вкусы в музыке, в то время как Себастей был необычайно одарен в этой области.

Ахилл : Мне очень нравится теория чисел. Не расскажете ли вы нам о каком-нибудь из открытий Себастея?

Муравьед : Отлично. (Делает паузу, чтобы отхлебнуть свой чай, и снова начинает.) Слышали ли вы о печально известной «Хорошо Проверенной Гипотезе» Фурми?

Ахилл : Не уверен. Это звучит знакомо, но я не могу вспомнить, что это такое.

Муравьед : Идея очень проста Француз Льер де Фурми, мураматик по призванию, но адвокей по профессии, читая классическую «Арифметику» Диофантея, наткнулся на страницу с уравнением

2 a+ 2 b= 2 c

Он тут же понял, что это уравнение имеет бесконечное множество решений a , b и с , и записал на полях следующий замечательный комментарий.

Уравнение

n a + n b = n c

имеет решение в положительных целых числах а , b , с , и n только при n = 2 (и в таком случае имеется бесконечное множество а , b , и с , удовлетворяющих этому уравнению), но для n >2 решений не существует. Я нашел совершенно замечательное доказательство этого — к несчастью, такое крохотное, что оно будет почти невидимо, если написать его на полях.

С того года и в течение почти трехсот дней мураматики безуспешно пытаются сделать одно из двух либо доказать утверждение Фурми и таким образом очистить его репутацию — в последнее время она слегка подпорчена скептиками, не верящими, что он действительно нашел доказательство — или опровергнуть его утверждение, найдя контрпример множество четырех целых чисел а , b , с , и n , где n > 2, которое удовлетворяло бы этому уравнению. До недавнего времени все попытки в любом из этих двух направлений проваливались. Точнее, Гипотеза доказана лишь для определенных значений n — в частности, для всех n до 125 000. Но никому не удавалось доказать ее для ВСЕХ n — никому, пока на сцене не появился Иогей Себастей Фермовей. Именно он нашел доказательство, очистившее репутацию Фурми. Теперь это известно под именем «Хорошо Проверенной Гипотезы Иогея Себастея Фермовея».

Рис. 63. Когда происходят перемещения колоний, муравьи иногда строят из собственных тел живые мосты. На этой фотографии (Льера Фурми) изображен подобный мост. Муравьи-работники колонии Eciton Burchelli сцепляются лапками и тарзальными челюстями; таким образом создается что-то вроде цепей. Видно, как по центру мосту переходит симбиотическая чешуйница, Trichatelura manni. (E. О. Вильсон, «Общества насекомых» (Е.О. Wilson, «The Insect Societies», стр. 62.)

Ахилл : Не лучше ли тогда называть это «Теоремой» вместо «Гипотезы,» поскольку настоящее доказательство уже найдено?

Муравьед : Строго говоря, вы правы, но по традиции это зовется именно так.

Черепаха : А какую музыку писал Себастей?

Муравьед : Он был очень талантливым композитором. К несчастью, его лучшее сочинение покрыто тайной, поскольку оно никогда не было опубликовано. Некоторые думают, что Себастей держал свое сочинение в голове. Но те, кто настроены менее благожелательно, говорят, что на самом деле он никогда не писал подобного сочинения, а только хвастался направо и налево.

Ахилл : И что же это было за великое сочинение?

Муравьед : Это должно было быть гигантской прелюдией и фугой; в фуге предполагалось двадцать четыре голоса и двадцать четыре различных темы, по одной в каждом мажорном и минорном ключе.

Ахилл : Было бы весьма трудно слушать такую двадцатичетырехголосную футу как целое!

Краб : Уже не говоря о том, чтобы ее сочинить!

Муравьед : Все, что нам о ней известно, это ее описание, оставленное Себастеем на полях его экземпляра «Прелюдий и фуг для органа» Букстехуде. Последними словами, которые он написал перед своей трагической кончиной, были следующие:

Я сочинил замечательную фугу. В ней я соединил силу 24 тональностей с силой 24 тем, получилась фуга с мощью в 24 голоса. К несчастью, она не помещается на полях.

Этот несостоявшийся шедевр известен под именем «Последняя Фуга Фермовея».

Ахилл : О, как это невыносимо трагично!

Черепаха : Кстати о фугах: та фуга, которую мы слушаем, скоро закончится. Ближе к концу в ее теме происходит странная вариация. (Переворачивает страницу «Хорошо темперированного клавира».) Что это у нас тут? Еще одна иллюстрация, да какая интересная! (Показывает ее Крабу.)

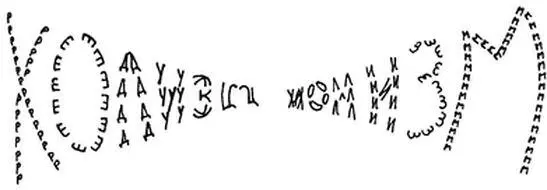
Рис. 64. (Рисунок автора. Русский графический вариант выполнен переводчиком.)

Краб : Что это у нас тут? О, вижу это «ХОЛИЗМИОНИЗМ», написанное большими буквами, которые сначала уменьшаются, а затем снова возрастают до того же размера. Но в этом нет никакого смысла, поскольку это не настоящее слово. Надо же, подумать только! (Передает ноты Муравьеду)

Муравьед : Что это у нас тут? О, вижу: это «РЕДУКЦХОЛИЗМ», написанное маленькими буквами, которые сначала увеличиваются, а затем снова уменьшаются до того же размера. Но в этом нет никакого смысла, поскольку это не настоящее слово. Подумать только, надо же! (Передает ноты Ахиллу.)

Ахилл : Я знаю, что никто из вас в это не поверит, но на деле эта картинка состоит из слова «ХОЛИЗМ», написанного дважды, причем буквы в нем уменьшаются слева направо.

Черепаха : Я знаю, что никто из вас в это не поверит, но на деле эта картинка состоит из слова «РЕДУКЦИОНИЗМ», написанного один раз, причем буквы в нем увеличиваются слева направо.