Даглас Хофштадтер - ГЕДЕЛЬ, ЭШЕР, БАХ: эта бесконечная гирлянда

Ахилл : Вы намекаете на то, что Кэйджу место в зверинце? Что ж, если учесть, что его фамилия в переводе с английского значит «клетка»… Но вернемся к крабьему музыкальному автомату — я ничего не понимаю. Как могут на одной и той же записи быть сразу В-А-С-H и C-A-G-E?

Черепаха : Если вы посмотрите повнимательней, Ахилл, вы можете подметить, что между ними есть некоторая связь. Вот, взгляните: что у вас получится, если вы последовательно запишете интервалы мелодии В-А-С-H?

Ахилл : Ну-ка, посмотрим… Сначала она понижается на полтона, от В до А (я имею в виду немецкое В); затем поднимается на три полутона до С, и, наконец, опускается на полутон, до H. Получается следующая схема:

-1, +3, -1

Черепаха : Совершенно верно. А как насчет C-A-G-E?

Ахилл : Здесь мелодия сначала идет на три полутона вниз, потом поднимается на десять полутонов, и снова опускается на три полутона. Получается:

-3, +10, -3

Очень похоже на первую мелодию, правда?

Черепаха : Действительно, похоже. В некотором смысле, у этих двух мелодий совершенно одинаковый «скелет». Вы можете получить C-A-G-E из В-А-С-H, умножив все интервалы на 3,5 и беря ближайшее целое число.

Ахилл : Вот это да! Это значит, что на звуковых дорожках записан только некий основной код, который разные проигрыватели интерпретируют по-разному?

Черепаха : Я не уверена — этот уклончивый Краб не посвятил меня во все детали. Но мне удалось услышать третью песню, произведенную на проигрывателе В-10.

Ахилл : И как она звучала?

Черепаха : Ее мелодия состояла из огромных интервалов: В-С-А-H.

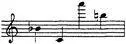
Схема в полутонах была такая:

-10, +33, -10

Эта мелодия получается из C-A-G-E, если снова умножить интервалы на 3,3 и округлить результаты до ближайшего целого числа.

Ахилл : Есть ли какое-то название у такого умножения интервалов?

Черепаха : Его можно назвать «интервальным увеличением». Оно похоже на прием ритмического увеличения темы канона. При этом длительность всех нот мелодии умножается на какое-либо постоянное число. В результате мелодия замедляется. Здесь же интересным образом расширяется диапазон мелодии.

Ахилл : Удивительно. Так что все три мелодии, что вы услышали, были интервальными увеличениями одной и той же схемы звуковых дорожек?

Черепаха : Таково мое заключение.

Ахилл : Забавно, когда мы увеличиваем В-А-С-H, у нас получается C-A-G-E, a когда мы опять увеличиваем C-A-G-E, то снова получаем В-А-С-H, только теперь он весь перевернут, словно В-А-С-H разнервничался, проходя через промежуточный этап C-A-G-E.

Черепаха : Поистине, глубокий комментарий к этой новой форме искусства — музыке Кэйджа.

В ПОСЛЕДНЕЙ ГЛАВЕ, мы сформулировали вопрос. «Когда две вещи похожи друг на друга?» В этой главе мы рассмотрим оборотную сторону этого вопроса. «Когда одна и та же вещь не похожа сама на себя?» Мы попытаемся выяснить, присуще ли значение самому сообщению или же оно всегда порождается взаимодействием разума (или механизма) с этим сообщением — как в предыдущем Диалоге. В последнем случае нельзя было бы сказать ни что значение находится в каком-то одном месте, ни что сообщение имеет некое универсальное или объективное значение — поскольку каждый наблюдатель привносил бы в каждое сообщение свое собственное значение. Но в первом случае значение имело бы постоянное место и было бы универсально. В этой главе я постараюсь показать универсальность по крайней мере некоторых сообщений, не утверждая этого для всех сообщений вообще. Как мы увидим, идея «объективности значения» некоего сообщения интересным образом соотносится с тем, насколько легко может быть описан разум.

Начну с моего любимого примера отношения между пластинками, музыкой и проигрывателями. Мы привыкли к мысли о том, что пластинка содержит ту же информацию, что и музыкальное произведение, так как существуют проигрыватели, которые способны «читать» записи и превращать структуру звуковых дорожек в звуки. Иными словами, между звуковыми дорожками и звуками существует изоморфизм, проигрыватель — механизм, осуществляющий этот изоморфизм физически. Таким образом, естественно думать о пластинках как о носителях информации и о проигрывателях, как об обнаружителях информации . Другой пример этих понятий — система pr. Там «носителями информации» являлись теоремы, а ее «обнаружителем» была интерпретация, такая прозрачная, что для извлечения информации из теорем нам не понадобились никакие электронные машины.

Эти два примера наводят на мысль, что изоморфизмы и декодирующие механизмы (то есть, обнаружители информации) всего лишь «проявляют» информацию, уже имеющуюся в структуре сообщения и только ждущую своего часа, чтобы быть извлеченной. Отсюда следует, что в любой структуре есть некая информация, которую возможно извлечь, так же как и информация, которую извлечь нельзя . Но что именно означает фраза «извлечь информацию»? С какой силой нам позволено ее «вытягивать»? В некоторых случаях, приложив достаточно усилий, удается извлечь очень глубоко запрятанную информацию. На самом деле, извлечение информации может потребовать настолько сложных операций, что вам может показаться, что вы вкладываете больше информации, чем извлекаете.

Рассмотрим пример генетической информации, содержащейся в двойной спирали дезоксирибонуклеиновой кислоты (ДНК). Молекула ДНК — генотип — превращается в физический организм — фенотип — путем весьма сложного процесса, включающего выработку белков, воспроизведение ДНК, воспроизведение клеток, постепенное различение типов клеток, и т. д. Процесс превращения генотипа в фенотип — эпигенез — представляет собой пример наиболее запутанной из запутанных рекурсий; мы уделим ему все внимание в главе XVI. Эпигенез зависит от множества сложнейших химических реакций и петель обратной связи. К тому времени, когда создание организма закончено, его физические характеристики не имеют ни малейшего сходства с его генотипом.

Тем не менее, считается, что физическая структура организма восходит к его ДНК — и только к ней. Впервые это подтвердили эксперименты Освальда Авери, проведенные в 1944 году; с тех пор собрано много убедительных данных в пользу этой идеи. Эксперименты Авери показали, что из множества молекул только ДНК обладает свойством передавать наследственные качества. Можно изменить другие молекулы в организме, например, белки, но эти изменения не будут переданы последующим поколениям. Однако когда меняется ДНК, изменения наследуются всеми последующими поколениями. Эти эксперименты доказали, что единственный способ изменить инструкции по построению нового организма заключается в изменении его ДНК; из этого, в свою очередь, следует, что эти инструкции должны быть закодированы где-то в структуре ДНК.