Морис Клайн - Математика. Утрата определенности.

Превращение всей математики, за исключением разве лишь теории целых чисел, в геометрию привело к нескольким важным последствиям. Прежде всего оно усилило разрыв между теорией чисел и геометрией, ибо несоизмеримые величины целиком подлежали юрисдикции геометрии — арифметике (теории чисел) они были, так сказать, «неподсудны». Со времен Евклида между теорией чисел и геометрией приходилось проводить резкую границу. {63}А поскольку геометрия охватывала значительную часть математики, именно она и стала (по крайней мере до XVII в.) основой почти всей «строгой» математики. Мы до сих пор называем x 2 «икс квадратом», x 3 — «икс кубом», а не x соответственно во второй и в третьей степени, потому что некогда под x 2 и x 3 понимался лишь геометрический смысл этих величин.

Разумеется, геометрическое представление чисел и операций над ними не очень подходило для практических целей. Логически вполне удовлетворительно представлять произведение √2∙√3 как площадь прямоугольника. Но если требуется вычислить это произведение, то такого представления явно недостаточно. В естествознании и технике геометрические фигуры значительно менее полезны, чем численный ответ, полученный с требуемой точностью. В приложениях математики и в технике интерес представляют главным образом количественные результаты. Судоводителю в открытом море необходимо знать местоположение судна — численные значения его координат в градусах широты и долготы. Чтобы строить прочные и надежные здания, мосты, суда и плотины, также необходимо знать количественные меры длин, площадей и объемов деталей каждого сооружения. Более того, количественные характеристики, размеры, деталей сооружения необходимо знать заранее, до того как начнется постройка. Но греки классического периода, превыше всего ценившие строгие рассуждения и с пренебрежением относившиеся к приложениям математики в торговых расчетах, навигации, строительстве и составлении календарей, были удовлетворены полученным геометрическим решением проблемы иррациональных чисел.

На смену греческой цивилизации эпохи высокой классики (афинский период) около III в. до н.э. пришла эпоха эллинизма (александрийский период), сложившаяся в результате слияния классической греческой культуры с культурами Египта и Вавилона (гл. I). С точки зрения логики математика александрийского периода представляла собой любопытное смешение дедуктивных и эмпирических подходов. Наиболее выдающиеся математики александрийской эпохи Архимед и Аполлоний следовали образцу аксиоматической, дедуктивной геометрии «Начал» Евклида. Даже в своих трудах по механике Архимед начинал с аксиом и доказывал теоремы, став предтечей Ньютона и его последователей, создавших «математическую физику». Но под влиянием более прагматичных египтян и вавилонян александрийцы начали использовать математику и для удовлетворения запросов практики. В Александрии были выведены формулы, позволяющие вычислять количественные меры длин, площадей и объемов. Так, Герон (I в.) в своем сочинении «Метрика» привел формулу для вычисления площади S треугольника. {64}

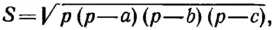
где a, b, c — длины сторон треугольника, p — его полупериметр. Вычисление площади треугольника по формуле Герона нередко приводит к иррациональным числам. Формула Герона замечательна еще в одном отношении: в отличие от греков эпохи высокой классики, которые считали бессмысленным произведение более чем трех чисел, поскольку ему нельзя было придать геометрический смысл, Герон был чужд подобных предрассудков. Во многих чистых и прикладных науках, развитых греческими учеными александрийского периода — составление календаря, измерение времени, навигационные расчеты, оптика, география, пневматика и гидростатика (гл. I), — иррациональные числа находили самое широкое применение.

Высшим достижением александрийцев стало создание Гиппархом и Птолемеем количественной астрономии — геоцентрической системы мира, позволившей человеку предсказывать движение планет, Солнца и Луны (гл. I). Для построения своей количественной теории Гиппарх и Птолемей разработали тригонометрию — область математики, занимающуюся вычислением одних элементов треугольника по данным о других его элементах. Так как подход Птолемея к построению тригонометрии отличался от принятого в то время, ему пришлось вычислять длины хорд окружности. Хотя для получения основных результатов об отношениях длин одних хорд к длинам других Птолемей использовал дедуктивно-геометрический метод, в процессе вычислений длин хорд (а именно они и были конечной целью расчетов) он широко применял арифметику и зачатки алгебры. Длины большинства хорд выражались иррациональными числами. Птолемей довольствовался получением рациональных приближений нужных ему величин, но в ходе вычислений, не колеблясь, употреблял и иррациональные числа.

Арифметика и алгебра, столь свободно используемые александрийцами, которым они достались по наследству от египтян и вавилонян, были лишены логической основы. Птолемей и другие ученые александрийского периода, как правило, перенимали у древних египтян и вавилонян эмпирический подход к математике. Такие иррациональные числа, как π , √2, √3 и другие, вводились некритически и в случае необходимости заменялись рациональными приближениями. Наиболее известный пример использования иррациональных чисел — приближенное вычисление Архимедом числа π. По оценкам Архимеда, значение π заключено между 3 1/ 7и 3 10/ 71. Независимо от того, знал или нет Архимед, что число π иррационально, найденные им приближенные значения π содержали нескончаемые нагромождения квадратных корней ([33], с. 266-270, 528-553), а извлечение квадратного корня чревато появлением иррациональных чисел, о чем не мог не знать Архимед.

Для нашего повествования возрождение александрийскими математиками египетской и вавилонской алгебры, не зависящей от геометрии, имеет ничуть не меньшее значение, чем свободное использование иррациональных чисел. Выдающуюся роль в «оживлении» старой традиции сыграли Герон и еще один представитель александрийской школы — Диофант (примерно III в.). И Герон, и Диофант считали, что алгебраические и арифметические задачи представляют самостоятельный интерес и что обращение к геометрии излишне, поскольку не придает ни большей значимости задачам, ни большей логичности решениям. Герон формулировал и решал алгебраические задачи чисто арифметическими средствами. Например, дан квадрат, такой, что сумма его площади и периметра равна 896 {65}; требуется найти сторону квадрата. Чтобы решить квадратное уравнение, к которому сводится задача, Герон добавляет к обеим частям полученного равенства по 4 и извлекает из них квадратный корень. Герон не доказывает правильности своих действий, а лишь указывает, в какой последовательности их надлежит выполнить. В работах Герона имеется немало задач такого рода.