Морис Клайн - Математика. Утрата определенности.

Рис. 1.1.Треугольные числа.

Рис. 1.2.Квадратные числа.

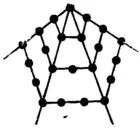
Рис. 1.3.Пятиугольные числа.

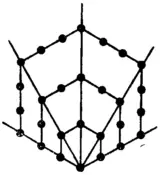
Рис. 1.4.Шестиугольные числа.

Хотя дошедшие до нас фрагменты исторических документов не позволяют установить точную хронологию событий, не вызывает сомнения, что пифагорейцы, развив и усовершенствовав свои учения, начали рассматривать числа как абстрактные понятия, а объекты — как конкретные реализации чисел. Именно в смысле такого более позднего различия, по-видимому, надлежит понимать высказывание знаменитого пифагорейца V в. до н.э. Филолая: «Если бы ни число и его природа, ничто существующее нельзя было бы постичь ни само по себе, ни в его отношении к другим вещам… Мощь чисел проявляется, как нетрудно заметить… во всех деяниях и помыслах людей, во всех ремеслах и музыке».

Свести музыку к простым отношениям чисел пифагорейцам удалось после того, как они совершили два открытия: во-первых, что высота тона, издаваемого колеблющейся струной, зависит от ее длины и, во-вторых, что гармонические созвучия издают одинаково натянутые струны, длины которых относятся между собой как целые числа ([5], с. 393-434). Например, гармоническое созвучие издают две одинаково натянутые струны, из которых одна вдвое длиннее другой. На современном языке интервал между тонами, издаваемыми такими двумя струнами, называется октавой. Другое гармоническое созвучие издают две струны, длины которых относятся как 3:2. В этом случае более короткая струна издает ноту, которая на квинту выше тона, издаваемого более длинной струной. Пифагорейцы разработали знаменитую музыкальную шкалу. Мы не будем, подробно останавливаться на музыке греческого периода. Заметим лишь, что многие греческие математики, в том числе Евклид и Птолемей, посвятили музыке, в частности гармоническим созвучиям и построению музыкальной шкалы, специальные сочинения.

Движения планет пифагорейцы также свели к числовым отношениям. Они считали, что тела, двигаясь в пространстве, издают звуки. Должно быть, на эту мысль их навело наблюдение: камень, раскручиваемый на веревке, со свистом разрезает воздух. Пифагорейцы полагали, что быстро движущееся тело издает более высокий звук, чем тело, движущееся медленно. Согласно астрономическим воззрениям пифагорейцев, планеты движутся тем быстрее, чем дальше они находятся от Земли. Звуки, издаваемые планетами, изменяются в зависимости от удаления от Земли и образуют гармоническое созвучие. Но эта «музыка сфер», подобно всякой гармонии, сводится к числовым отношениям, поэтому и движения планет также сводятся к числовым отношениям. Мы не слышим музыку небесных сфер потому, что привыкли к ней с самого рождения.

Другие явления природы также были сведены пифагорейцами к числам. Особую роль в учении пифагорейцев играли числа 1, 2, 3 и 4, образовывавшие тетрактис, или четверицу. По преданию, клятва пифагорейцев гласила: «Клянусь именем Тетрактис, ниспосланной нашим душам. В ней источник и корни вечно цветущей природы». Пифагорейцы считали, что все объекты в природе состоят из четверок, таких, как четыре геометрических элемента: точка, линия, поверхность и тело. Впоследствии Платон придавал особое значение четверке материальных элементов: земле, воздуху, огню и воде.

Сумма чисел, входящих в тетрактис, равна десяти, поэтому десять считалось идеальным числом и символизировало Вселенную. А поскольку число десять идеально, то в небесах должно было быть ровно десять тел. Поэтому пифагорейцы ввели центральный огонь, вокруг которого обращаются Земля, Солнце, Луна и пять известных в древности планет, а также Противоземля, расположенная по другую сторону от центрального огня. Центральный огонь и Противоземля невидимы, потому что поверхность Земли, на которой мы живем, скрывает их от нас. Вряд ли уместно входить в детали пифагорейской картины мира. Главное заключается в том, что пифагорейцы пытались построить астрономическую теорию на основе числовых отношений.

После того как пифагорейцы «свели» астрономию и музыку к числу, музыка и астрономия оказались связанными с арифметикой и геометрией и все четыре дисциплины стали считаться математическими. Они вошли в программу общего образования, причем это положение сохранилось вплоть до средневековья. В средние века комплекс общеобразовательных дисциплин, состоящий из арифметики, геометрии, музыки и астрономии, получил название квадривиум.

Общий итог пифагорейского отождествления числа и реального мира подведен в «Метафизике» Аристотеля:

В числах пифагорейцы усматривали (так им казалось) много сходного с тем, что существует и возникает, — больше, чем в огне, земле и воде (например, такое-то свойство чисел есть справедливость, а такое-то — душа и ум, другое — удача, и, можно сказать, в каждом из остальных случаев точно так же); так как далее они видели, что свойства и соотношения, присущие гармонии, выразимы в числах; так как, следовательно, им казалось, что все остальное по природе своей явно уподобляемо числам и что числа — первое во всей природе, то они предположили, что элементы чисел суть элементы всего существующего и что все небо есть гармония и число.

Натурфилософию пифагорейцев лишь с большой натяжкой можно назвать состоятельной. Эстетические соображения, к которым примешивается навязчивое стремление найти числовые соотношения, не могли не приводить к утверждениям, выходящим за пределы реальных наблюдений. Пифагорейцам не удалось сколько-нибудь существенно продвинуть ни одну из областей физической науки. С полным основанием их теории можно было бы назвать поверхностными. Но то ли по счастливому стечению обстоятельств, то ли благодаря гениальной интуиции пифагорейцам удалось сформулировать два тезиса, общезначимость которых подтвердило все последующее развитие науки: во-первых, что основополагающие принципы, на которых зиждется мироздание, можно выразить на языке математики; во-вторых, что объединяющим началом всех вещей служат числовые отношения, которые выражают гармонию и порядок природы. Современная наука разделяет пифагорейскую приверженность числу, хотя, как мы увидим далее, современные теории представляют собой гораздо более искусную форму пифагореизма.