Морис Клайн - Математика. Утрата определенности.

A есть p ;

B есть p .

Следовательно, А и В суть p.

Действительно, рассуждение

Джон — брат,

Питер — брат;

следовательно, Джон и Питер братья (каждый доводится братом другому)

вполне может привести к неправильному заключению, если понятие «брат» расширить, включив в него и двоюродного брата. Аристотелевой логике не удалось построить логику отношений. На этот ее недостаток обращал внимание еще Лейбниц.

Отношения далеко не всегда удается перевести на язык субъекта и предиката, когда предикат лишь утверждает, что субъект принадлежит к задаваемому предикатом классу. Часто бывает необходимо рассматривать и такие утверждения, как «2 меньше 3» или «Точка Q лежит между точками P и R ». Для подобных высказываний также необходимо определять, что означает их отрицание, т.е. обратное утверждение, сложное высказывание, составленное из нескольких таких высказываний, и т.д.

Логика отношений была развита в серии статей, опубликованных в 1870-1893 гг. Чарлзом Сандерсом Пирсом (1839-1914), и систематизирована Эрнстом Шредером (1841-1902). Пирс ввел специальную символику для обозначения высказываний, выражающих отношения. Так, символ l ij означает, что i любит j . Построенная Пирсом алгебра была сложной и малополезной. Позднее мы увидим, как рассматривает отношения современная математическая логика.

Пирс внес в науку логики еще одно важное дополнение, которое лишь слегка затронул Буль; он подчеркнул важность пропозициональных функций (функций-высказываний). Подобно тому как в математике мы рассматриваем функции, например y = 2x, отличая их от утверждений о конкретных числовых равенствах типа 10 = 2∙5, так высказывание «Джон — человек» вполне конкретно, а высказывание « x — человек» означает пропозициональную функцию, зависящую от переменной x. Пропозициональные функции могут зависеть от двух и большего числа переменных: такова, например, функция « x любит y ». Результаты Пирса позволили распространить логику и на пропозициональные функции.

Пирс ввел в логику и так называемые кванторы. Обычный язык неоднозначен по отношению к кванторам. В двух высказываниях:

Американец возглавлял войну за независимость;

Американец верит в демократию

субъект «американец» используется в двух различных смыслах: в первом высказывании речь идет о вполне конкретном лице — Джордже Вашингтоне, во втором — о любом американце. Обычно неоднозначность можно уменьшить, сославшись на контекст, в котором используется предложение, но в строгом логическом мышлении такая неоднозначность недопустима. Смысл высказывания должен быть ясен без всяких ссылок на контекст. Кванторы позволяют достичь однозначности высказываний. Мы можем утверждать, что какая-то пропозициональная функция истинна для всех индивидуумов из определенного класса, например для всех граждан США. В этом случае высказывание «Для всех x, x — люди» означает «Все граждане США — люди». Слова «для всех x » — квантор. Но мы можем также утверждать: существует по крайней мере один x, такой, что x — человек из США. В этом случае квантор — это слова «существует по крайней мере один x, такой, что». Каждый из этих типов кванторов имеет специальное обозначение: в первом случае 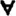x (квантор общности), во втором x (квантор существования).

Включение в логику отношений пропозициональных функций и кванторов позволило существенно расширить ее. Охватив те типы рассуждений, которые используются в математике, логика стала более полной.

Последний шаг в математизации логики в XIX в. был сделан профессором математики Йенского университета Готлобом Фреге (1848-1925). Его перу принадлежит несколько фундаментальных трудов: «Исчисление понятий» (1879), «Основания арифметики» (1884) и «Основные законы арифметики» (т. I — 1893, т. II — 1903). Восприняв идеи логики высказываний, логики отношений, пропозициональные функции и кванторы, Фреге внес свой вклад в развитие математической логики. Он ввел различие между простым утверждением высказывания и утверждением, что данное высказывание истинно. В последнем случае Фреге ставил перед высказыванием знак |—. Фреге проводил также различие между объектом x и множеством {x}, содержащим только x, между элементом, принадлежащим множеству, и включением одного множества в другое.

Фреге формализовал более широкое понятие импликации — так называемую материальную импликацию, хотя следы этого понятия в неформализованной, словесной форме можно проследить вплоть до Филона из Мегары (около III в. до н.э.). {97}Логика имеет дело с рассуждениями относительно высказываний и пропозициональных функций, и весьма важная роль в этих рассуждениях отводится импликации. Так, если мы знаем, что Джон мудр и что мудрые люди живут долго, то с помощью импликации заключаем, что Джон будет жить долго.

Материальная импликация несколько отличается от обычно используемой импликации. Когда мы говорим, например, «Если пойдет дождь, то я отправлюсь в кино», между двумя высказываниями «Пойдет дождь» и «Я отправлюсь в кино» существует не просто какое-то отношение, а именно импликация: если антецедент (высказывание, стоящее в условном высказывании между «если» и «то») истинен, то из него с необходимостью следует консеквент (высказывание, стоящее в условном высказывании после «то»). Но в материальной импликации антецедентом p и консеквентом q могут быть любые высказывания. Между ними не обязательно должна существовать причинно-следственная связь и даже вообще какое бы то ни было отношение. Так, ничто не мешает нам рассматривать материальную импликацию «Если x — нечетное число, то я пойду в кино». Эта импликация ложна только в том случае, если x — нечетное число, а я все равно не отправлюсь в кино.

На более формальном языке это означает, что если p и q — высказывания и p истинно, то из истинности импликации «Если p, то q » («из p следует q », или « p влечет за собой q ») мы вправе заключить, что q также истинно. Если же p ложно, то независимо от того, ложно или истинно q, материальная импликация «Если p, то q » считается истинной. И только в том случае, если p истинно, a q ложно, импликация считается ложной. Понятие материальной импликации расширяет привычное употребление связки «если …, то …». Но такое расширение не приводит к каким-либо затруднениям, так как обычно мы используем импликацию «если p , то q », только когда знаем, что p истинно. Кроме того, материальная импликация в какой-то мере согласуется с тем смыслом, который мы обычно вкладываем в условные высказывания «Если …, то …». Рассмотрим предложение «Если Гарольд получит сегодня жалованье, то он купит продукты». Здесь p — высказывание «Гарольд получит сегодня жалованье», q — высказывание «Он купит продукты». Но Гарольд может купить продукты, даже если он не получит сегодня жалованье. Следовательно, импликацию «Если p, то q» мы можем считать истинной и в том случае, когда p ложно, a q истинно. Другим, возможно еще лучшим, примером разумности такого решения может служить условное предложение «Если бы дерево было металлом, то дерево было бы ковким». Мы знаем, что оба высказывания (и антецедент, и консеквент) ложны, тем не менее вся импликация в целом истинна. Следовательно, если p ложно и q ложно, то импликацию «Если p, то q» также надлежит считать истинной. Понятие материальной импликации находит важное применение, позволяя судить об истинности q по истинности p и импликации «Если p, то q ». Обобщение на случай, когда p ложно, удобно для математической логики и представляется наиболее разумным из всех вариантов.