Морис Клайн - Математика. Поиск истины.

Читая научные сочинения Кеплера, не устаешь удивляться полету его фантазии. Как и Коперник, Кеплер был глубоко верующим человеком и, подобно Копернику, был убежден, что при сотворении мира Бог следовал какому-то простому и изящному математическому плану. «Господь Бог был слишком благостен, чтобы пребывать в праздности, и принялся забавляться различными знаками, запечатляя свой образ и подобие в этом мире. Исходя их этого, я полагаю, что искусство геометрии символизирует всю природу и прекрасное небо», — писал Кеплер. В своем первом сочинении «Космографическая тайна» (1596) он поставил целью доказать, что математические гармонии, которыми руководствовался Создатель при сотворении мира, есть «сущность трех вещей — почему они устроены так, а не иначе…: число, размеры и движения небесных орбит» ([11], с. 176). Глубокое убеждение в существовании гармонии мира наложило отпечаток на все мышление Кеплера.

При всей своей экзальтированности Кеплер был наделен качествами, которые у нас принято связывать с учеными. Он мог быть предельно рациональным. Его богатое воображение рождало одну за другой новые теоретические схемы, но Кеплер понимал, что теория должна согласоваться с результатами наблюдений, а в последние годы жизни еще более отчетливо сознавал, что эмпирические данные способны привести к открытию фундаментальных принципов науки. Именно поэтому Кеплер с готовностью жертвовал самыми, казалось бы, многообещающими математическими гипотезами, если видел, что они не согласуются с наблюдательными данными, и с невероятным упорством отказывался мириться с малейшими отклонениями, которыми любой из современных ученых с легкостью бы пренебрег, если бы речь шла о подтверждении его радикальных идей. Кеплер обладал скромностью, терпением и энергией, которые помогают великим людям вершить их непомерный труд.

Наиболее значительные свои работы Кеплер выполнил в те годы, когда был астрономом при дворе императора Рудольфа. Движимый красотой и гармонией системы Коперника, Кеплер решил посвятить себя поиску дополнительных геометрических гармоний, скрытых в результатах многолетних астрономических наблюдений Тихо Браге, и попытаться найти математические соотношения между всеми явлениями природы. Однако пристрастие подгонять природу к заранее придуманной математической схеме стоило Кеплеру нескольких лет безуспешных поисков «гармонии мира». В предисловии к «Космографической тайне» он сформулировал свою основную задачу следующим образом:

В этой книжке я вознамерился доказать, что всеблагой и всемогущий Бог при сотворении нашего движущегося мира и при расположении небесных орбит избрал за основу пять правильных тел, которые со времен Пифагора и Платона и до наших дней снискали столь громкую славу, выбрал число и пропорции небесных орбит, а также отношения между движениями в соответствии с природой правильных тел.

Следуя своему плану, Кеплер постулировал, что радиусы орбит шести планет совпадают с радиусами сфер, связанных с пятью правильными (Платоновыми) телами следующим образом. Самый большой радиус имеет сфера Сатурна. В нее вписан куб. В этот куб вписана сфера, радиус которой есть радиус сферы Юпитера. В сферу Юпитера вписан тетраэдр, а в тетраэдр в свою очередь вписана сфера, радиус которой есть радиус сферы Марса, — и так для всех пяти правильных тел. В результате такого построения Кеплер получил шесть сфер — по числу известных тогда планет (рис. 23). Вскоре Кеплер понял, что его теория при всем своем изяществе не точна. Хотя вычисленные им расстояния между орбитами планет были очень близки к истинным, все же расстояния между сферами последовательно вписанными в правильные тела и описанными вокруг правильных тел, не вполне точно соответствовали расстояниям между планетами.

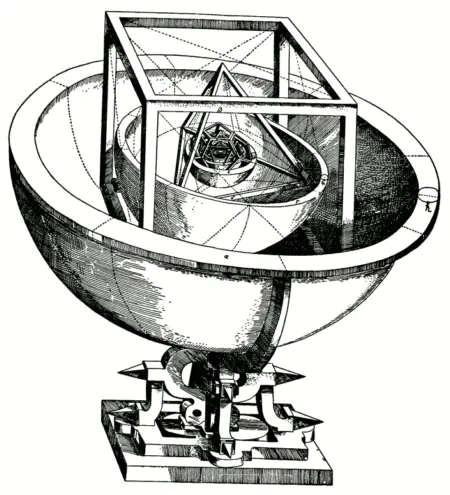
Рис. 23.

До этого момента к работе Кеплера в полной мере относилось критическое замечание, которое Аристотель не раз адресовал пифагорейцам: «Они [пифагорейцы] рассматривали явления не ради их самих и не ради того, чтобы докопаться до их причин, а единственно с намерением подогнать явления под свои априорные суждения и попытаться реконструировать мир». Но умудренный опытом прошлых веков Кеплер слишком чтил факты, чтобы отстаивать теории, не согласующиеся с наблюдениями и не позволяющие делать точные, предсказания.

Получив в свое распоряжение данные многолетних наблюдений Тихо Браге и проведя собственные наблюдения, Кеплер убедился в необходимости отвергнуть астрономические построения как своих предшественников, Птолемея и Коперника, так и собственные. Неутомимый поиск законов, которые бы находились в согласии с данными наблюдений, увенчался открытием трех знаменитых законов движения планет. Первые два закона Кеплер изложил в своем труде «Новая астрономия», опубликованном в 1609 г.

Первый из законов Кеплера в полном противоречии с традицией вводит в астрономию эллипс. Изучением этой кривой занимались еще древние греки примерно за две тысячи лет до описываемых событий, поэтому математические свойства эллипса были хорошо известны. Если окружность можно определить как геометрическое место точек, равноудаленных (на расстояние, равное радиусу) от данной точки (центра окружности), то эллипс можно определить как геометрическое место точек, сумма расстояний от которых до двух заданных точек постоянна. Таким образом, если F 1 и F 2 — две заданные точки (рис 24), а P — произвольная точка эллипса, то сумма PF 1+ PF 2 не зависит от того, где именно расположена точка P на эллипсе. Две заданные точки F 1 и F 2 называются фокусами эллипса. Первый закон Кеплера гласит: каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. Другой фокус — чисто математическая точка, физически ничем не выделенная. Разумеется, каждая планета движется по своему эллипсу, один из фокусов которого (тот, в котором находится Солнце) является общим для эллиптических орбит всех планет. Таким образом, после пятнадцати столетий безуспешных попыток описать движение планет с помощью громоздких комбинаций окружностей на смену последним пришел простой эллипс.

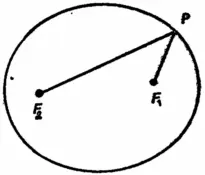
Рис. 24.

Первый закон Кеплера говорит нам, по какой траектории движется планета, но умалчивает о том, сколь быстро планета движется по своей орбите; когда бы мы ни наблюдали положение планеты, предсказать, через какое время она окажется в другой точке орбиты, нам не удастся. Можно было бы ожидать, что каждая планета движется по своей орбите с постоянной скоростью, но, как показывали наблюдения — а именно с ними прежде всего сверялся Кеплер, — такое предположение не соответствует действительности. Второй закон Кеплера утверждает, что площади, заметаемые за одинаковое время отрезком, проведенным от Солнца к планете, равны. Иначе говоря, если планета перемещается из точки P в точку Q (рис. 25), скажем, за один месяц и из точки P' в точку Q' также за один месяц, то площади секторов F 1PQ и F 2P 'Q ' равны. Кеплер был вне себя от радости, когда обнаружил, что закон изменения скоростей выражается столь простой зависимостью. Всевидящий Бог явно отдавал предпочтение постоянной секторной скорости перед постоянной линейной скоростью.