Алексей Лосев - Хаос и структура

Однако, прежде чем перейти в сферу выразительности, еще необходимо перейти от становления к ставшему, к выражению внутреннего через отвлеченное задание, т. е. перейти к пределу. Последнее дано в определении континуума у Кантора при помощи моментов плотности в себе и замкнутости, входящих в понятие совершенного множества. Поскольку в этих моментах речь не просто о непрерывности, но и о пределах, момент ставшего уже оказывается включенным.

Однако и этого мало. В континууме Кантора даны не только предельные точки, они сами тоже вовлечены в новый поток становления, поскольку в нем мыслится еще и <���…> связность. Но когда мы говорили об энергийно–выразительном, или эманативном моменте числа, мы как раз и мыслили становление, но не то становление, когда смысл впервые только еще вступает в свое инобытие и в нем погасает, но такое становление, когда смысл снова нашел себя в инобытии, растворился в нем, расцвел в нем и на нем, когда становление стало снова (…) включивши в себя, однако, и смысловой результат всех своих субстанциональных положений. Момент связности в Канторовом континууме, заставляющий сливаться в непрерывность уже не просто отдельные точки множества, но именно все его предельные точки, и демонстрирует для нас эту энергийную выразительность, которой не было в непрерывности на ступени ее идеально–бытийственной структуры.

с) Таким образом, в Канторовом континууме мы находим по крайней мере три различных диалектических слоя, совпадающих с обычной триадой: идеальный слой едино–раздельной структуры (полнота и сцепленность), реальное становление ее, или переход в инобытие (сцепленность), и — через ставшее как момент предела (плотность в себе и замкнутость)—синтез того и другого (связность), когда идеальная непрерывность снова находит себя в бесконечно–предельном процессе инобытия (связное совершенное множество).

d) Сравнивая это учение с постулатом Дедекинда, мы не можем не заметить явного превосходства учения Кантора над Дедекиндом. В то время как у Дедекинда (и Кантора) в постулате непрерывности имеется в виду ее обрисованность, ее зрительно–мотивированный переход от одного качества к другому, в учении Кантора о континууме подчеркнут момент понимания выразительного слоя непрерывности. Ведь здесь эта непрерывность вся перекрыта предельными точками. Это значит, что вся она состоит из точек, притягивающих к себе, из точек–идеалов, из точек–целей, из тех эманаций, которые своим исхождением из сущности привлекают к ней, вовлекают в свою стихию и своим привлечением к сущности всего чужого заставляют исходить ее вовне <���…> бесконечными энергиями исхождения. Если под аксиомой непрерывности Дедекинда лежит интуиция разноцветных, но непрерывно взаимопереливающихся полей, то Кантор, строя свое учение о континууме, несомненно, исходил (может быть, тайно от себя самого) из образа таких же полей, но скомбинированных в ту или иную фигурную предметность, т. е. из той непрерывности, которая свойственна реальной комбинации реальных же вещей.

Когда мы рассматриваем, напр., цветок, то уже по одному тому, что он есть нечто целое, он есть и нечто в себе непрерывное. Тем не менее мы видим на нем несколько разных красок, напр. желтое на пурпурном и все вместе — на зеленом стебле, и мы видим тут много разных оттенков одного и того же цвета. Если бы мы просто фиксировали все это разнообразие, как собрание взаимно–изолированных вещей или красок, для нас достаточно было бы в смысле конструирования непрерывности [39] Так в рукописи. уже аксиомы Архимеда (§ 59.4). Если бы мы отвлеклись от всякой раздельной предметности и рассматривали бы цветок, не обращая внимания на стебель, листья, чашечку и пр., а исключительно только бы с точки зрения непрерывного перехода одного цвета в другой, нам достаточно было бы аксиомы Дедекинда и Кантора о непрерывности. Но когда каждый момент рассматриваемого цветка фиксируется не просто сам по себе, но как притягивающий к себе, заставляющий фиксировать именно его, когда он целесообразно группирует вокруг себя все прочее и является целью для всех других моментов, другими словами, когда вся эта непрерывность есть непрерывность пределов, тогда возникает континуум Кантора; и тогда перед нами начинает расстилаться непрерывность фигуры цветности, а не просто самой цветности; тогда перед нами та непрерывность в цветке, в букете, в человеческом лице, в разноцветном небе раннего солнечного восхода или позднего заката, — словом, везде, где разнообразие цветностей вызвано тем или другим прерывно–смысловым, а не чисто же цветностным принципом. Есть ведь какая–то непрерывность, разлитая по всему букету, несмотря на всю его раздельность и многоразличие входящих в него цветов. И ее не может не быть, так как, прервись она хотя бы на одно мгновение, букет уже распался бы на две или больше различных вещей. И вот эта–то — уже фигурная — непрерывность и есть континуум Кантора. Это и в диалектически–терминологическом, и в житейски–буквальном смысле выразительная, энергийная, эманативная, понимаемая непрерывность [40] Учение о континууме Г. Кантор формулировал в «Основах общего учения о многообразиях». Рус. пер. в «Нов. идеях в математике». СПб., 1914. № 6. § 10. .

3. Что касается теории вероятностей, то категория непрерывности тут имеет гоже богатое применение, хотя, кажется, здесь и не дано столь ярких формулировок, как в теории множеств. Самым отвлеченным и самым примитивным теоретико–вероятностным пониманием непрерывности является то, что здесь называют геометрической вероятностью.

Основной интуицией для этой последней является линия или плоскость и составленность того или другого из точек. Если наша вероятность такова, что число возможных случаев равно числу возможных положений точки на прямой или на плоскости (или числу положений прямой в пространстве и т. п.), то такая вероятность будет непрерывной. Если бы мы стали спрашивать, какова вероятность вообще положения точки Μ на прямой Л В, то эта задача ввиду непрерывности данной прямой была бы вполне неопределенна. Но мы можем на данной прямой взять какой–нибудь отрезок и сравнивать вероятность положения точки Μ на с длиной <1 CD> и <1 AB> Тогда задача получает определенность и мы сможем выставить такой принцип: вероятность того, чтобы точка Μ оказалась на определенном отрезке прямой А В, пропорциональна длине этого отрезка. Отсюда следствие: если Μ во что бы то ни стало находится на А В, т.е. вероятность этого ее нахождения равна единице, то вероятность ее нахождения на (CD) равна< >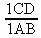

Этот принцип непрерывной вероятности дает возможность решать массу задач, например, хотя бы знаменитую задачу о попадании иглы в ту или иную параллель [линий], начерченных на горизонтальной плоскости (задача эта была решена еще Бюффоном). Большинство задач подобного рода требует, однако, применения методов интегрального исчисления.