Яков Перельман - Математика для любознательных

Это не что иное, как цена вещи без запроса, которую торговец для памяти обозначает на товаре, но так, однако, чтобы ее не мог разгадать покупатель. Бросив взгляд на эти буквы, торговец сразу проникает в их скрытый смысл и, сделав надбавку, называет покупателю цену с запросом.

Такая система обозначения весьма проста, - если только знать «ключ» к ней. Торговец выбирал какое-нибудь слово, составленное из 10 различных букв; чаще всего останавливали выбор на словах: трудолюбие, правосудие, ярославецъ, миролюбецъ, Миралюбовъ. Первая буква слова означает - 1, вторая - 2, третья - 3 и т. д.; десятою буквою обозначается нуль. С помощью этих условных букв-цифр торговец и обозначает на товарах их цену, храня в строгом секрете «ключ» к своей системе обозначения.

Если, например, выбрано слово:

правосудие

1234567890,

то цена 4 р. 75 к. будет обозначена так:

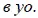
Знак « пое » означает 1 р. 50 к. (150), пее - 1 рубль (100) и т. п.

Иногда цена на товаре бывает написана в виде дроби; например, на одной из купленных мною книг имеется обозначение

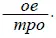
Это значит, при ключе «трудолюбие», что надо запросить 1 р. 25 коп., себе же книга стоила 50 коп.

Секрет своей меты торговцы строго берегут. Но если купить в одном и том же магазине несколько вещей, то, сопоставляя названную торговцем цену с соответствующими обозначениями, нетрудно догадаться о значении букв. Особенно легко разгадывать меты дешевых товаров, где запрашивают немного, так что первые цифры уплаченных сумм отвечают начальным буквам обозначения. Разгадав же несколько букв, легко доискаться значения остальных. При некоторой проницательности может быть разгадан «ключ» любой меты.

Допустим, например, что вы купили несколько вещей и заплатили за первую 25, за вторую - 22, за третью - 28 копеек. В уголках этих предметов вы находите такие обозначения

ро, рр, рд.

Ясно, что буква р означает 2. Отгадав, по другим товарам, еще одну букву, - например, с = 6, вы уже догадаетесь, что ключ - правосудие. Число подходящих слов, надо заметить, ограничено, и выбор не бывает чересчур затруднительным.

После сказанного легко сообразить, что числа можно изображать не только с помощью цифр, но и с помощью любых иных знаков или даже предметов - карандашей, перьев, линеек, резинок и т. п.; надо только условиться приписывать каждому предмету значение какой-нибудь определенной цифры. Можно даже, ради курьеза, с помощью таких цифр-предметов изображать действия над числами - складывать, вычитать, умножать, делить. Вот, например, ряд действий над числами, обозначенный предметами сервировки стола (см. рис.). Вилка, ложка, нож, кувшинчик, чайник, тарелка - все это знаки, каждый из которых заменяет определенную цифру.

Глядя на эту группу ножей, вилок, посуды и т. п., попробуйте угадать: какие именно числа здесь обозначены?

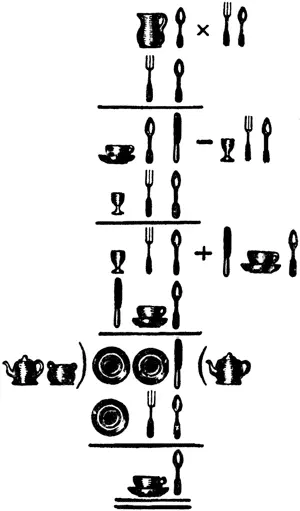
С первого взгляда такая задача кажется очень трудной: приходится разгадывать настоящие иероглифы, как сделал некогда француз Шамполион. Но ваша задача гораздо легче: вы ведь знаете, что числа здесь, хотя обозначены вилками, ножами, ложками и т. п., написаны по десятичной системе счисления, т. е. вам известно, что тарелка, стоящая на втором месте (считая справа), есть цифра десятков, что предмет направо от нее - цифра единиц, а по левую сторону - цифра сотен. Кроме того, вы знаете, что расположение всех этих предметов имеет определенный смысл, который вытекает из сущности арифметических действий, производимых над обозначенными ими числами. Все это может значительно облегчить вам решение предложенной задачи.

Вот как можно доискаться значения расставленных здесь предметов. Рассматривая первые три ряда на нашем рисунке, вы видите, что «ложка», умноженная на «ложку», дает «нож». А из следующих рядов видно, что «нож» без «ложки» дает «ложку», или что «ложка» + «ложка» = «ножу». Какая же цифра дает одно и то же и при удвоении и при умножении само на себя? Это может быть только 2, потому что 2 x 2 = 2 + 2. Таким образом узнаем, что «ложка» = 2 и, следовательно, «нож» = 4.

Теперь идем дальше. Какая цифра обозначена «вилкой»? Попробуем разгадать это, присмотревшись к первым трем рядам, где «вилка» участвует в умножении, и к рядам III, IV и V, где та же «вилка» фигурирует в действии вычитания. Из группы вычитания вы видите, что отнимая, в разряде десятков, «вилку» от «ложки», получаем в результате «вилку», т. е. при вычитании два минус «вилка» получается «вилка». Это может быть в двух случаях: либо «вилка» = 1, и тогда 2-1 = 1; либо же «вилка» = 6, и тогда, вычитая 6 из 12 (единица высшего разряда занимается у «чашки»), получаем 6.

Что же выбрать: 1 или 6? Испытаем, годится ли 6 для «вилки» в других действиях. Обратите внимание на сложение V и VI рядов: «вилка» (т. е. 6) + «чашка» = «тарелке»; значит, «чашка» должна быть меньше 4 (потому что в рядах VII и VIII «тарелка» минус «вилка» = «чашке»). Но «чашка» не может равняться двойке, так как двойка обозначена уже «ложкой»; не может «чашка» быть и единицей - иначе вычитание IV ряда из III не могло бы дать трехзначного числа в V ряду. Не может, наконец, «чашка» обозначать и 3 - вот почему: если «чашка» = 3, то «бокальчик» (см. ряды IV и V) должен обозначать единицу; потому что 1 + 1 = 2, т. е. «бокальчик» + «бокальчик» = «чашке», убавленной на единицу, которая была занята у него при вычитании в разряде десятков; «бокальчик» же равняться единице не может, потому что тогда «тарелка» в VII ряду будет обозначать в одном случае цифру 5 («бокальчик» + «нож»), а в другом цифру 6 («вилка» + «чашка»), чего быть не может. Значит, нельзя было допустить, что «вилка» = 6, а надо было принять ее равной единице.

Узнав путем таких - довольно, правда, долгих, - поисков, что «вилка» обозначает цифру 1, мы дальше уже идем более уверенно и быстро. Из действия вычитания в III и IV рядах видим, что «чашка» обозначает либо 6, либо 8. Но 8 приходится отвергнуть, потому что тогда вышло бы, что «бокальчик» - 4, а мы знаем, что цифра 4 обозначена «ножом». Итак, «чашка» обозначает цифру 6, а следовательно, «бокальчик» - цифру 3.

Какая же цифра обозначена «кувшинчиком» в I ряду? Это легко узнать, раз нам известно произведение (III ряд, 624) и один из множителей (II ряд, 12). Разделив 624 на 12, получаем 52. Следовательно, «кувшинчик» = 5.