Яков Перельман - Математика для любознательных

Но и это еще не все. Умножьте число 142857 на 2, на 3, на 4, на 5 или на 6 - и вы получите снова то же число, лишь передвинутое, в круговом порядке, на одну или несколько цифр:

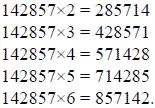
Чем же обусловлены все загадочные особенности этого числа?

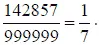
Мы нападаем на путь к разгадке, если продлим немного последнюю табличку и попробуем умножить наше число на 7: в результате получится 999999. Значит, число наше - не что иное, как седьмая часть 999999, а, следовательно, дробь И действительно, если вы станете превращать 1/7 в десятичную дробь, вы получите:

Наше загадочное число есть период бесконечной периодической дроби, которая получается при превращении 1/ 7в десятичную. Становится понятным теперь, почему при удвоении, утроении и т. д. этого числа происходит лишь перестановка одной группы цифр на другое место. Ведь умножение этого числа на 2 делает его равным 2/ 7и, следовательно, равносильно превращению в десятичную дробь уже не 1/ 7, а 2/ 7. Начав же превращать дробь 2/ 7в десятичную, вы сразу заметите, что цифра 2 - один из тех остатков, которые у нас получались уже при превращении 1/ 7; ясно, что должен повториться и прежний ряд цифр частного, но он начнется с другой цифры; иными словами, должен получиться тот же период, но только несколько начальных цифр его очутятся на конце. То же самое произойдет и при умножении на 3, на 4, на 5 и на 6, т. е. на все числа, получающиеся в остатках. При умножении же на 7 мы должны получить целую 1-цу, или, - что то же самое - 0,9999…

Любопытные результаты сложения и вычитания чисел на кольцах находят себе объяснение в том же факте, что 142857 есть период дроби, равной 1/ 7. В самом деле: что мы делаем, поворачивая кольцо на несколько цифр? Переставляем группу цифр спереди на конец, т. е., согласно только что сказанному, мы умножаем число 142857 на 2, на 3, на 4 и т. д. Следовательно, все действия сложения или вычитания чисел, написанных на кольцах, сводятся к сложению или вычитанию дробей 1/ 7, 2/ 7, 3/ 7и т. д. В результате мы должны получить, конечно, несколько седьмых долей, - т. е. опять-таки наш ряд цифр 142857 в той или иной круговой перестановке. Отсюда надо исключить лишь случаи, когда складываются такие числа седьмых долей, которые в сумме дают 1 или больше 1.

Но и последние случаи исключаются не вполне: они дают результат, правда, не тождественный с рассмотренными, но все же сходный с ними. Рассмотрим внимательнее, что должно получиться от умножения нашего загадочного числа на множитель больше 7, т. е. на 8, на 9 и т. д. Умножить 142857, например, на 8, мы можем так: умножить сначала на 7 и к произведению (т. е. к 999999) прибавить наше число:

142857 x 8 = 142857 x 7 + 142857 = 999999 + 142857 = 1.000.000-1 + 142857 = 1.000.000 + (142857-1).

Окончательный результат - 1142856 - отличается от умножаемого 142857 только тем, что впереди стоит еще одна 1-ца, а последняя цифра на 1-цу же уменьшена. По сходному правилу составляются произведения 142857 на всякое другое число, больше 7, - как легко усмотреть из следующих строк:

142857 x 8 = (142857 x 7) + 142857 = 1142856

142857 x 9 = (142857 x 7) + (142857 x 2) = 1285713

142857 x 10 = (142857 x 7) + (142857 x 3) = 1428570

142857 x 16 = (143857 x 7 x 2) + (142857 x 2) = 2285712

142857 x 39 = (142857 x 7 x 5) + (142857 x 4) = 5571423.

Общее правило здесь такое: при умножении 142857 на любой множитель нужно умножить лишь на остаток от деления множителя на 7; впереди этого произведения ставится число, показывающее, сколько семерок в множителе, и то же число вычитается из результата [67]. Пусть мы желаем умножить 142857 на 86. Множитель 86при делении на 7 дает в частном 12 и в остатке 4. Следовательно, результат умножения таков:

12571428 - 12 = 12571416.

От умножения 142857 x 365 мы получим (так как 365 при делении на 7 дает в частном 52, а в остатке 1):

52142857 - 52 = 52142805.

Усвоив это простое правило и запомнив результаты умножения нашего диковинного числа на множители от 2 до 6 (что весьма нетрудно - нужно помнить лишь, с какой цифры они начинаются), вы можете изумлять непосвященных молниеносно-быстрым умножением шестизначного числа. А чтобы не забыть этого удивительного числа, запомним, что оно произошло от 1/ 7, или - что то же самое, - от 2/ 14; вот вам первые три цифры нашего числа: 142. Остальные три получаются вычитанием первых трех из 9-ти:

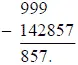
Мы уже имели дело с такими числами - именно, когда знакомились со свойствами числа 999. Вспомнив сказанное там, мы сразу сообразим, что число 142857 есть, очевидно, результат умножения 143 на 999:

142857 = 143 x 999.

Но 143 = 13 x 11. Припомнив замеченное раньше о числе 1001, равном 7 x 11 x 13, мы будем в состоянии, не выполняя действия, предсказать, что должно получиться от умножения 142857 x 7:

142857 x 7 = 143 x 999 x 7 = 999 x 11 x 13 x 7 = 999 x 1001 = 999999

(все эти преобразования мы, конечно, можем проделать в уме).

Только что рассмотренное нами число 142857 является одним из членов целой семьи чисел, обладающих теми же свойствами. Вот еще одно такое число: 058823594117647 (0 впереди необходим). Если умножить это число, например, на 4, мы получим тот же ряд цифр, только первые 4 цифры будут переставлены в конец:

0588235294117647x4 = 2352941176470588.

Расположив цифры этого числа на ряде подвижных колец, как в предыдущем случае, - мы при сложении чисел двух колец будем получать то же число, лишь смещенное в круговом порядке:

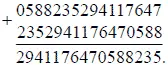
При кольцевом расположении все три ряда, конечно, тождественны.

От вычитания чисел двух колец опять-таки получается тот же круг цифр:

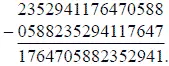
Наконец, это число, как и рассмотренное ранее, состоит из двух половин: цифры второй половины являются дополнением цифр первой половины до 9.

Попробуйте найти разгадку всех этих особенностей.

Нетрудно догадаться, каким образом приведенный числовой ряд оказался столь близким родственником числа 142857; последнее число представляет собою период бесконечной дроби, равной 1/ 7, наше же число является, вероятно, периодом какой-нибудь другой дроби. Так и есть: наш длинный ряд цифр - не что иное, как период бесконечной дроби, получающейся от превращения в десятичную простой дроби 1/ 17:

1/ 17= 0,(0588235294117647).