Майкл Шермер - Магия чисел. Ментальные вычисления в уме и другие математические фокусы

Приближенная оценка квадратного корня из шестизначного числа вроде 593 472 может показаться невозможной для непосвященного. Но вы даже не успеете устать. Так как 700 2= 490 000 и 800 2= 640 000, квадратный корень из 593 472 должен находиться между 700 и 800. На самом деле все пяти- и шестизначные числа имеют трехзначные квадратные корни. На практике вам нужно извлечь квадратный корень только из первых двух цифр шестизначного числа (или из первой цифры пятизначного). Выяснив, что квадратный корень из 59 лежит между 7 и 8, вы определите, что ответ равен «700 плюс…».

Теперь перейдем к привычному способу представления.

Квадратный корень из 593 472 равен 770,37, так что вы довольно близки к правильному решению. Но можно приблизиться еще больше. Как это сделать, покажет следующий прием.

Обратите внимание, что первые две цифры 59 ближе к 64 (8 х 8), чем к 49 (7 х 7). Благодаря этому можно начать оценку с цифры 8 и продолжить, отталкиваясь от нее.

Просто ради забавы сделаем что-нибудь с настоящей громадиной: извлечем квадратный корень из 28 674 529. Это не так трудно, как может показаться. Первый шаг — округление до наибольшего ближайшего числа. В данном случае надо просто найти квадратный корень из 29.

Все семизначные и восьмизначные числа имеют четырехзначные квадратные корни. Таким образом, 5,4 становится 5400 — это оценка. А более точный ответ — 5354,8. Неплохо!

На этом мы завершим главу о приближенных оценках в математике. После выполнения упражнений, представленных в ее конце, переходите к следующей главе о математике с ручкой и бумагой: вы научитесь записывать ответы в задачах быстрее, чем делали это раньше.

* * *

Математическая дуэль Эвариста Галуа

Трагическая история французского математика Эвариста Галуа (1811–1832), убитого в возрасте двадцати лет на дуэли из-за «печально известной кокетки», стала легендарной в истории математики. Не по годам развитый блестящий студент, Галуа заложил основу для раздела математики, известного как теория групп. Легенда гласит, что он изложил на бумаге эту теорию в ночь перед дуэлью, предвидя кончину и желая оставить свое наследие математическому сообществу. За несколько часов до смерти 30 мая 1832 года Галуа написал Огюсту Шевалье: «Я сделал несколько новых открытий в анализе.

Первое касается теории уравнений, остальные — интегральных функций». После этого он попросил друга: «Обратитесь с публичной просьбой к Якоби или Гауссу, чтобы высказали свое мнение не по поводу истинности, а насчет важности этих теорем. Я надеюсь, что кому-нибудь покажется интересным и полезным разобраться в этом беспорядке».

Романтическая легенда и историческая правда, однако, не всегда совпадают. То, что Галуа написал в ночь перед смертью, представляло собой исправления и редакторские правки в документах, принятых Академией наук задолго до этого. Более того, первоначальные документы Галуа были представлены за три года до дуэли, когда ему исполнилось всего семнадцать!

Именно после этого он оказался втянутым в политический конфликт, был арестован, провел какое-то время в темнице и в конечном счете ввязался в ссору из-за женщины и был убит.

Осознавая свою преждевременную зрелость, Галуа отмечал: «Я проводил исследования, которые остановят других ученых». На протяжении более чем ста лет так и происходило.

В главе 0 мы рассказывали, как в большинстве случаев проще вычислить сумму чаевых. Например, чтобы подсчитать 10 % чаевых, надо всего-навсего умножить счет на 0,1 (или поделить его на 10). Например, если счет равен 42 долларам, то 10 % чаевых составят 4,20 доллара. Для вычисления 20 % чаевых надо просто умножить счет на 0,2 или удвоить величину 10 % чаевых. Так, 20 % чаевых по счету в 42 доллара будут равны 8,40 доллара.

Для вычисления 15 % чаевых имеется несколько приемов. Если вы освоили техники из главы 2 и подружились с умножением, то вы просто можете умножить сумму счета на 15 и затем поделить полученный результат на 100. Например, при счете 42 доллара: 42 х 15 = 42 х 5 х 3 = 210 х 3 = 630, что легко делится на 100 и дает чаевые в размере 6,30 доллара. Другой метод: взять среднее от 10 % и 20 % чаевых. В соответствии с нашими ранними вычислениями это выглядит так:

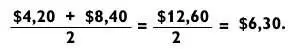
Наверное, самый популярный способ подсчета 15 % чаевых состоит в том, чтобы взять 10 % от общего счета, поделить их на два (что соответствует 5 %), а затем сложить полученные значения. Например, при счете 42 доллара надо сложить 4,20 доллара и половину этой величины, то есть 2,10 доллара:

4,20 + 2,10 = 6,30.

Применим все три метода, чтобы вычислить 15 % от счета в 67 долларов. Прямой метод: 67 х 3 х 5 = 201 х 5 = 1005, что при делении на 100 дает 10,05 доллара. Метод усреднения: усредняем 10 % чаевых в виде 6,70 доллара и 20 % в виде 13,40 доллара и получаем:

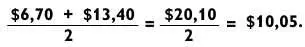
Используя последний метод, прибавляем 6,70 доллара к половине данной величины, равной 3,35 доллара, чтобы получить

6,70 + 3,35 = 10,05.

Наконец, для подсчета 25 % чаевых мы предлагаем два метода. Либо умножьте сумму на 25, а затем разделите на 100, либо разделите сумму на 4 (возможно, путем двойного деления числа на два). Например, при счете в 42 доллара можно вычислить 42 х 25 = 42 х 5 х 5 = 210 х 5 = 1050, что при делении на 100 дает чаевые в размере 10,50 доллара. Или можно разделить исходную величину на 4, или сократить ее наполовину дважды: половина 42 долларов — 21 доллар, и еще пополам — 10,50 доллара. При счете в 67 долларов я бы, вероятно, разделил прямо на 4: так как 67 ÷ 4 = 16 3/4, получаем 25 % чаевых в размере 16,75 доллара.

В этом разделе я продемонстрирую метод устной оценки величины налога с продаж. Для некоторых налоговых ставок, таких как 5 %, или 6 %, или 10 %, требуются прямые вычисления.

Например, чтобы посчитать налог 6 %, нужно просто умножить цену на 6 и разделить на 100. Допустим, цена составляет 58 долларов, тогда 58 х 6 = 348, что при делении на 100 дает точный размер налога с продаж 3,48 доллара. (При этом общая сумма будет равна 61,48 доллара.)

Но как посчитать налог в 6,5 % от 58 долларов? Я покажу вам несколько способов, как это сделать, а вы выберете тот, который покажется вам наиболее приемлемым. Наверное, самый легкий способ прибавить полпроцента к любой сумме в долларах состоит в ее делении пополам и последующем переводе в центы. В примере с 58 долларами их половина составляет 29. Поэтому просто прибавьте 29 центов к 6 % налога (уже посчитанным 3,48 доллара) и получите налог в размере 3,77 доллара.