Жуан Гомес - Мир математики. т.2. Математики, шпионы и хакеры. Кодирование и криптография

С (а, b)(х) = (ах+ b)= y (mod n)

(ах+ b)= у (mod n)

ах— у— b (mod n)

Другими словами, нам нужно найти значение а -1(обратное значению а ), удовлетворяющее равенству а -1а= 1, так что

а -1 ах= а -1 х(у— b)(mod n)

х= а -1 (у— b)(mod n).

Следовательно, для успешной расшифровки мы должны найти число, обратное числу а по модулю n , и, чтобы не тратить зря время, мы должны заранее знать, существует ли это обратное число.

В случае аффинного шифра С (а, b)(х)= (ах+ b) (mod n)обратное значение числа абудет существовать тогда и только тогда, когда НОД ( а, n) = 1.

В случае аффинного шифра в нашем примере, С(х)= 2х+ 1 (mod 6), мы хотим узнать, существует ли обратное значение для числа а, в нашем случае для числа 2.

То есть существует ли целое число n, которое меньше 6 и удовлетворяет выражению 2∙ n= 1 (mod 6). Для ответа на этот вопрос мы подставим в данное выражение все возможные значения (0, 1, 2, 3, 4, 5):

2-0 = 0, 2–1 = 2, 2–2 = 4, 2–3 = 6 0, 2–4 = 8 2, 2–5 = 10 4.

Нет такого значения, следовательно, можно заключить, что 2 не имеет обратного числа. На самом деле мы это уже знали, так как НОД (2,6) 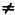1.

Предположим теперь, что мы перехватили зашифрованное сообщение: YSFMG. Мы знаем, что оно было зашифровано аффинным шифром вида С( х) = 2 х+ 3 и изначально было написано на испанском языке с алфавитом из 27 букв (включая букву N, идущую после обычной N).

Как получить исходное сообщение?

Сначала мы посчитаем НОД (2,27), который равен 1. Значит, сообщение можно расшифровать! Для этого для функции С( х) = 2 х+ 3 мы должны найти обратную функцию по модулю 27:

у= 2х+ 3

2х= у— 3.

Чтобы найти x, мы должны умножить обе части уравнения на число, обратное 2.

Число, обратное числу 2 по модулю 27, — это целое число n такое, что 2 n 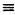1 (mod 27), а именно 14. И действительно:

14∙2 = 28 1.

Итак, мы имеем

x = 14∙(у— 3).

Теперь мы можем расшифровать сообщение YSFMG.

Буква Yстоит на позиции 25, ей соответствует расшифрованная буква, стоящая на позиции

14∙(25—3) = 308 11 (mod 27).

Буква, стоящая в алфавите на позиции 11, — это L.

Для буквы Sимеем 14∙(19—3) = 224 8 (mod 27), эта позиция соответствует букве I.

Для буквы Fимеем 14∙(5–3) = 28 1 (mod 27), что соответствует букве В.

Для буквы Мимеем 14∙(12—3) = 126 18 (mod 27), что соответствует букве R.

Для буквы Gимеем 14∙(6–3) = 42 15 (mod 27), что соответствует букве О.

Расшифрованное сообщение является испанским словом LIBRO, что означает «книга».

Различные системы безопасности на протяжении многих веков использовали идею Цезаря и ее обобщение в виде аффинного шифра. В настоящее время любой шифр, в котором каждая буква исходного сообщения заменяется на другую букву, сдвинутую на фиксированное число позиций (не обязательно три), называется шифром Цезаря.

Одним из существенных достоинств хорошего алгоритма шифрования является способность генерировать большое количество ключей. И шифр Цезаря, и аффинный шифр уязвимы для криптоанализа, поскольку максимальное количество ключей ограничено.

Если мы снимем какие-либо ограничения относительно порядка букв шифроалфавита, то потенциальное количество ключей резко возрастет. Количество ключей для стандартного алфавита из 26 символов (расположенных в произвольном порядке) составляет 26! = 403291461126605635584000000, то есть более 403 септиллионов ключей. Криптоаналитику, который тратит на проверку одного ключа всего лишь одну секунду, потребуется в миллиард раз больше времени, чем ожидаемое время существования Вселенной, чтобы исчерпать все возможности!

Вот один из примеров такого обобщенного шифра подстановки:

Строка (1) — алфавит открытого сообщения. Строка (2) — шифроалфавит.

Первые шесть букв шифроалфавита дают подсказку к выбранному порядку букв: он соответствует порядку букв на клавиатуре в стандарте QWERTY. Чтобы зашифровать известное высказывание Цезаря VENI VIDI VICI («Пришел, увидел, победил») шифром QWERTY, для каждой буквы алфавита открытого сообщения мы найдем соответствующую в шифроалфавите.

Мы получим следующее зашифрованное послание:

CTFO CORO СОЕО

Существует очень простой способ для генерации почти неисчерпаемого количества легко запоминающихся шифров для шифрования этим методом. Достаточно выбрать любое ключевое слово (это может быть даже фраза), поместить его в начале шифроалфавита и, начиная с последней буквы ключевого слова, завершить ряд буквами стандартного алфавита, следующими в обычном порядке, исключив лишь повторяющиеся буквы. Возьмем в качестве примера ключевую фразу JANUARY CIPHER («январский шифр»). Сначала мы избавимся от пробела и одинаковых букв, получив ключевое слово JNUYCIPHE. В результате наш шифроалфавит будет выглядеть так:

Сообщение VENI VIDI VICI теперь будет зашифровано как ХСМЕ XEYE XEUE. Такая система генерации шифров легко обновляется и почти исключает ошибки со стороны отправителя и получателя. В нашем примере было бы достаточно менять ключевое слово каждый месяц — JANUARY CIPHER (январский шифр), FEBRUARY CIPHER (февральский шифр), MARCH CIPHER (мартовский шифр) и т. д. — то есть после изначального выбора шифра стороны могут обойтись без дополнительных соглашений.

Надежность и простота алгоритма шифра подстановки с использованием ключевых слов сделали его самой распространенной системой шифрования на протяжении многих веков. В прежние времена считалось, что криптографы все-таки взяли верх над криптоаналитиками.

* * *

ШИФРОВАНИЕ СЛОВА БОЖЬЕГО

Средневековые криптоаналитики считали, что в Ветхом Завете тоже использовались шифры, и они не ошиблись. Существует несколько фрагментов из священных текстов, которые зашифрованы с помощью шифра подстановки, называемого атбаш. Этот шифр состоит в замене каждой буквы ( n) другой буквой, которая находится в алфавите на таком же расстоянии от конца алфавита, как оригинальная буква — от начала. Например, в латинском алфавите буква Азаменяется на Z, буква В— на Yи т. д. В оригинальном Ветхом Завете использовались буквы еврейского алфавита. Так, в книге пророка Иеремии (25:26) слово «Бабель» (Вавилон) зашифровано как «Шешах».