Игнаси Белда - Том 33. Разум, машины и математика. Искусственный интеллект и его задачи

Все эти факторы препятствовали появлению признаков, которые были присущи похожим видам, обитавшим в более конкурентных средах.

В отсутствие хищников и при избытке пропитания в изолированной экосистеме острова додо не нужны были сильные крылья и мощные лапы. Кстати, в дословном переводе с португальского «додо» означает «глупый». Кто знает, возможно, додо стали «глупыми» именно из-за того, что отсутствовало давление отбора?

Додо на гравюре XVII века.

Следующий этап эволюционного алгоритма, выполняемый после оценки особей текущего поколения, — это отбор. Его цель — выделить лучших особей, которые оставят потомство. Процесс отбора лучших особей является основой естественной эволюции. Интенсивность этого процесса называется давлением отбора. Давление отбора тем больше, чем меньше доля особей, переходящих в следующее поколение.

Однако можно доказать, что если мы применим столь простую стратегию, как прямой отбор лучших особей, то давление отбора будет слишком велико. При значительном давлении отбора эволюционные алгоритмы обычно работают не слишком хорошо, так как завершают работу на локальных, а не глобальных оптимумах.

Главное преимущество эволюционных алгоритмов — возможность получить хорошие решения на больших областях поиска, или, говоря математическим языком, возможность найти оптимумы функций, как правило, многомерных и имеющих несколько локальных или глобальных максимумов. Если давление отбора при эволюционной оптимизации слишком велико, то есть если мы хотим найти решение слишком быстро, для чего выберем лучших особей и ограничимся поверхностным рассмотрением, то алгоритм завершит работу слишком рано, а его результатами будут локальные, а не глобальные оптимумы.

Этап отбора идеально подходит для моделирования давления отбора в эволюционных алгоритмах. В пределе, когда давление отбора будет наибольшим, производится единичный отбор — иными словами, из текущего поколения выбирается только одна особь, на основе которой образуется следующее поколение. Другим предельным случаем будет полностью случайный отбор, при котором приспособленность особей не учитывается. Логично, что следует выбрать некую промежуточную стратегию, при которой производится отбор лучших особей для размножения и вместе с тем присутствует некоторая степень случайности, позволяющая рассмотреть альтернативные варианты. При такой стратегии с определенной вероятностью может быть выбрана любая, даже самая неприспособленная особь. Сегодня применяются три стратегии отбора, обладающие этими свойствами: рулетка, ранговая селекция и турнирная селекция.

Метод селекции, основанный на принципе колеса рулетки, достаточно прост. Он заключается в том, что каждая особь может быть выбрана с вероятностью, пропорциональной ее приспособленности по отношению к приспособленности остальных особей. Следовательно, если нужно отобрать 10 особей, колесо рулетки потребуется вращать 10 раз.

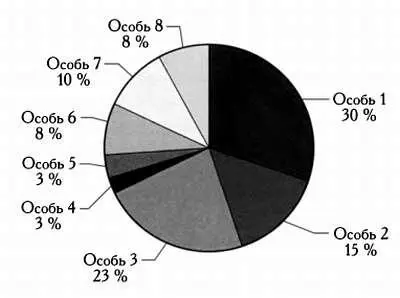
В примере на рисунке представлено восемь особей и значения их функции приспособленности в процентах от целого. Как вы можете догадаться, при каждом вращении рулетки вероятность выбора определенной особи будет пропорциональной отношению ее значения функции приспособленности к целому. Метод рулетки не исключает возможность выбора менее приспособленных особей — они всего лишь будут выбираться с меньшей вероятностью. Если мы будем вращать колесо рулетки 10 раз, то несколько раз обязательно выберем приспособленных особей, но также вероятно, что несколько раз выбранные особи будут не самыми конкурентоспособными. Именно возможность выбора неконкурентоспособных особей делает генетические алгоритмы столь мощными: это позволяет следовать несколькими путями одновременно, открывать другие варианты, выявлять множество различных максимумов, а в долгосрочной перспективе — находить хорошее локальное решение, а в лучшем случае — глобальный максимум.

Еще одна стратегия отбора, пригодная для решения сложных задач, — это ранговая селекция. При ее использовании отбирается nкопий наиболее приспособленной особи, n — 1 — второй по порядку и так далее до n= 0. Эта стратегия исключает вероятность того, что некая «сверхособь» снизит вероятность отбора прочих особей.

(«Сверхособью» называется особь, далекая от оптимальной, но намного превышающая по своим параметрам прочих особей из своего поколения.) Наличие сверхособей приводит к тому, что популяция оказывается скученной возле нее, и улучшить результаты становится невозможно.

Третья стратегия, турнирная селекция, заняла монопольное положение среди стратегий отбора, используемых при решении реальных задач, благодаря выгодным математическим свойствам и высокой гибкости при моделировании давления отбора. При турнирной селекции используется тот же принцип, что и при объединении спортивных команд в пары при игре на выбывание. Особи отбираются попарно случайным образом, и оптимальной считается та особь, которая побеждает в этом воображаемом турнире. Следовательно, при турнирной селекции необходимо отобрать столько пар, сколько особей необходимо выбрать. Почему эта стратегия считается очень гибкой при моделировании давления отбора? Что произойдет, если мы будем организовывать «турниры» не между двумя, а между nособями? Что если в турнире будет одерживать верх не одна, а mособей? В таком случае говорят, что проводится турнир n: m. С увеличением nдавление отбора будет повышаться, с увеличением m— понижаться.

Чтобы лучше понять схему проведения турнира, представьте себе начальные этапы футбольной Лиги чемпионов. Они проводятся по схеме 4:2 — футбольные команды объединяются произвольным образом в группы по четыре, а две лучшие переходят в следующий этап. Конечно, в примере с Лигой чемпионов нельзя говорить о действительно случайном турнире, так как при формировании групп учитываются определенные критерии — так, в одну группу не могут попасть две команды из одной страны. Однако мы тоже можем вводить свои правила при использовании эволюционных алгоритмов, что будет определять тот или иной тип эволюции.

Часто используется правило, согласно которому в одном турнире соперничают максимально похожие особи. Алгоритм способен находить оптимальные значения функции со множеством оптимумов.