Микель Альберти - Мир математики. т 40. Математическая планета. Путешествие вокруг света

Р (1,2) = Р (1,5) = 8/49 = 16,3 %.

Игроки понимают, что ставить на единственный исход слишком рискованно, и чаще ставят сразу на два числа.

Несколько вопросов, связанных с игрой, имеют отношение к доске, на которую бросают шарик. Первый вопрос касается формы самой доски: почему она квадратная? Второй вопрос имеет отношение к числу клеток: почему размер доски равен 7 x 7? Почему доска не имеет форму прямоугольника, треугольника, шестиугольника или круга? Разве нельзя играть на квадратной доске, разделенной на 25, 36 или 100 клеток?

Форма доски влияет на траекторию движения шарика, которая определяется направлением броска и отскоками от краев доски. Вопрос о форме доски относится к геометрии, вопрос о числе клеток — к алгебре. Теоретически возможны неслучайные броски, например когда траектория шарика представляет собой квадрат, соединяющий середины сторон доски. Такая траектория возможна в случае, когда мы бросаем шарик из любой точки над одной из сторон доски под углом в 45° к ней.

Но все это лишь теория — благодаря вогнутой форме клеток всякий раз, когда шарик не прокатывается точно по центру клетки, он отклоняется от траектории. В результате траектория оказывается случайной, и исход броска предугадать нельзя. Именно поэтому траектории, подобные ломаной линии, изображенной на доске серого цвета на рисунке ниже, невозможны.

Смоделировать траекторию шара на доске чисто математическими методами нельзя, для этого следует учесть физические факторы, в частности силу трения и силы, обусловленные вогнутой формой клеток, под действием которых траектория шарика при прохождении над клеткой меняется. Необходимость учитывать множество переменных крайне усложняет задачу, и можно считать, что исход игры является случайным.

Вопрос о числе клеток на доске, как мы уже говорили, относится к алгебре. Так как дано три фигуры и четыре цвета, образующие 12 сочетаний, и к ним нужно добавить еще одну клетку (когда шарик попадает на нее, все ставки уходят в банк), число клеток С должно быть на единицу больше числа, кратного 12:

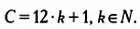
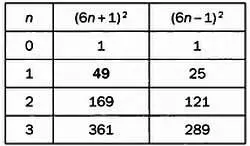
Учитывая, что доска должна иметь квадратную форму, С также должно быть квадратом натурального числа. Искомый результат достигается, если мы рассмотрим квадраты чисел, кратных 6, увеличенные или уменьшенные на единицу:

(6· λ ± 1) 2= 36· λ 2± 12 λ + 1 = 12 λ ·(3 λ ± 1) + 1 = 1 + число, кратное 12.

Число клеток на доске может быть и другим, но в этом случае вероятность выигрыша будет либо слишком низкой (при С > 49), либо слишком высокой ( С = 25).

В своей книге «Африка считает» Клаудия Заславски описывает игру, распространенную в народе кпелле. Игра начинается с того, что 16 камушков раскладываются в два ряда по восемь. Один из игроков загадывает камень, после чего другой игрок должен угадать, какой камень выбрал первый. Для этого он может не более четырех раз спросить, в каком из двух рядов находится выбранный камень. После каждого ответа второй игрок может переставлять камни из ряда в ряд.

Камни необязательно должны быть одинаковыми — для удобства их можно раскрашивать в разные цвета.

Чтобы одержать победу, нужно правильно переставлять камни после каждого ответа на вопрос. Допустим, что первый игрок выбрал камень под номером 13, но мы этого не знаем. Мы видим два ряда камней и спрашиваем: в каком ряду выбранный камень? Первый игрок ответит: в нижнем. Поменяем местами камни, стоящие на нечетных местах.

Повторив вопрос, мы узнаем, что теперь выбранный камень находится в верхнем ряду. Так как ранее камень располагался в другом ряду, мы знаем, что он принадлежит группе {9, 11, 13, 13}. Теперь переставим половину камней из этой группы, к примеру поменяем местами

Наш соперник ответит, что камень по-прежнему находится в первом ряду. Следовательно, он выбрал камень под номером 13 или 13. Переставим один из двух этих камней, например поменяем местами 13 и 5.

Выбранный нашим противником камень оказался во втором ряду, следовательно, мы можем ответить: камень номер 13.

Стратегия игры заключается в том, чтобы после каждого ответа менять местами в два раза меньше камней: сначала четыре, затем два и, наконец, один. Ответ на четвертый вопрос укажет решение. Эта стратегия работает потому, что исходные шестнадцать камней в начале игры уже разделены на два ряда. Когда противник говорит, в каком ряду находится выбранный камень, мы сразу же исключаем половину камней. Следовательно, если наша стратегия гарантирует, что после каждого ответа число вариантов уменьшается вдвое, мы обязательно придем к единственному решению:

16/2 = 8 —> 8/2 = 4 —> 4/2 = 2 —> 2/2 = 1

Несколько десятков тысяч лет назад человек решил покинуть природные укрытия и найти себе приют под крылом геометрических форм. Вместо того чтобы жить в пещерах, он обработал доступные природные материалы, придав им постоянную форму, и построил себе жилье. Форма жилища постепенно усложнялась.

Большинство современных домов представляют собой многогранники, чаще всего — прямоугольные призмы. Десятки и сотни семей в городах всего мира живут в колоссальных гексаэдрах, установленных вплотную друг к другу. Люди также живут или до недавнего времени жили в домах, где в явном или неявном виде присутствовал круг — дома имели форму цилиндра, конуса и даже сферы. Основная характеристика обитаемого гексаэдра — прямые углы: стены домов должны быть перпендикулярны земле и друг другу. Помещения в домах, а также большинство предметов мебели воспроизводят такую же модель. Многие столы, стулья, шкафы, стеллажи и кровати имеют форму гексаэдров, благодаря чему они идеально располагаются в любом месте комнаты. Более мелкие предметы, например лампы, отличаются большим разнообразием форм.

Также характерной особенностью народов и культур является объединение жилищ в группы. В некоторых культурах жилища располагаются в форме прямоугольника или круга, в других — не подчиняются какой-либо закономерности.