Микель Альберти - Мир математики. т 40. Математическая планета. Путешествие вокруг света

Папирус Ахмеса содержит 87 математических задач. Шесть первых посвящены делению чисел на 10, 16 задач посвящены суммам дробей, 18 — уравнениям, восемь — делению, 14 — вычислению объемов призм и усеченных пирамид, пять — вычислению площадей земельных участков и объемов тел вращения, а еще 15 относятся к экономике. Форма записи практически идентична той, что используется в современной математике, и если мы сравним папирус Ахмеса со школьными тетрадями, то не найдем между ними особых различий.

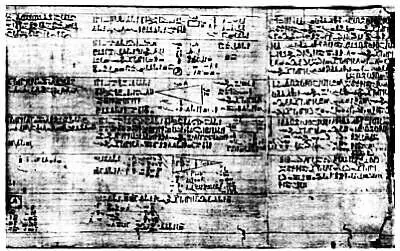
Папирус Ахмеса, один из древнейших математических текстов, дошедших до наших дней.

Египтяне также строили амбары цилиндрической формы и рассчитывали их вместимость через площадь круглого основания. Правило вычисления площади круга звучало так: «вычти из диаметра его девятую часть и возведи полученное число в квадрат».

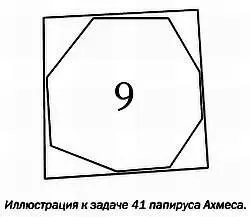
В задаче 41 требуется вычислить объем амбара с диаметром основания 9 локтей и высотой 10 локтей. Результат определяется умножением площади основания на высоту. При вычислении площади основания применяется указанное выше правило. Девятая часть от 9 локтей равна 1 локтю. Разность между ними равна 8 локтям. Возведя это значение в квадрат, получим 64 квадратных локтя. Умножив это число на 10, получим 640 кубических локтей. Точный ответ таков:

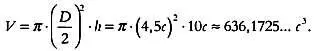
Результат, полученный по методу древних египтян, больше истинного всего на 0,6 %. Расхождение вызвано неявно используемым в этой формуле значением π — это единственное отличие египетской формулы от современной. Некоторые историки высоко оценивают древний метод именно потому, что в нем фигурирует достаточно точное значение π . Если мы сравним египетскую формулу с известной нам формулой площади круга, то увидим, что в ней соотношение между длиной окружности и ее диаметром, то есть π , принимается равным 3,16:

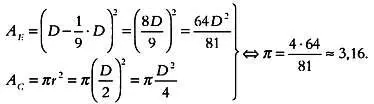
Однако внимания заслуживают два вопроса, которые, возможно, даже важнее, чем точность при вычислении π . Египтяне определяли объем фигуры как произведение площади ее основания на высоту. Как они пришли к этой формуле? Какие мысли, не зафиксированные в египетских папирусах, привели их к этой формуле?

По одной из гипотез, древние связывали площадь круга с площадью неправильного восьмиугольника, вписанного в квадрат стороной в 9 единиц.

Если мы хотим получить прямоугольную фигуру, по площади примерно равную кругу, то очевидно, что вписанный квадрат слишком мал, а описанный квадрат слишком велик. Среднее арифметическое площадей этих квадратов — не слишком точная оценка реальной площади круга, так как в ней число π принимается равным 3. Между прочим, именно такое значение π несколько веков использовалось в Древнем Египте и Месопотамии. Однако достаточно понаблюдать за тем, как колесо совершает полный оборот, чтобы убедиться: отношение длины окружности к ее диаметру очевидно больше 3.

Учитывая, что площади, в отличие от расстояний, нельзя измерить по земле, площадь круга можно оценить следующим образом: построить окружность, измерить ее длину, после чего вычислить ее по формуле и сравнить полученные результаты.

Какую формулу следует применить для расчета длины? Разумно ли принять длину окружности равной среднему арифметическому периметров вписанного и описанного квадрата? Возможно, да. Однако мы сталкиваемся еще с одной проблемой: найти периметр квадрата, вписанного в окружность, без теоремы Пифагора нельзя.

По одной из гипотез, египтяне принимали эквивалентным окружности неправильный восьмиугольник. Чтобы построить его, они делили стороны квадрата длиной в 9 единиц на три части каждую, для чего на сторонах квадрата отмечалось восемь точек. Далее эти точки соединялись линиями, и получался неправильный восьмиугольник, площадь которого визуально неотличима от площади круга.

Площадь круга равна 63,6 кв. ед. Площадь неправильного восьмиугольника отличается от нее менее чем на 1 %:

S k =9 2— 4·(1/2)·3 2= 81–18 = 63 кв. ед.

Еще одна гипотеза изложена в задаче папируса Ахмеса под номером 50. В ней площадь круглого поля диаметром 9 единиц принимается равной площади квадрата со стороной в 8 единиц. Автор папируса указывает, что подтверждение этого соотношения приводится в задаче 48. Задача 48 сопровождается рисунком, на котором изображен неправильный многоугольник, вписанный в квадрат. В центре обеих фигур записана цифра 8. Однако рисунок неточен: вписанный многоугольник имеет не восемь, а всего семь сторон, при этом одна из его сторон не полностью совпадает со стороной квадрата. Но здесь важно другое: почему египтяне думали, что круг диаметром 9 единиц эквивалентен квадрату со стороной 8 единиц?

С точки зрения современного человека площади этих фигур действительно схожи:

S 8 = π· 4,5 2= 63,617… кв. ед.

Их подобие нетрудно видеть на рисунке.

S квадрата = 8 2= 64 кв. ед.

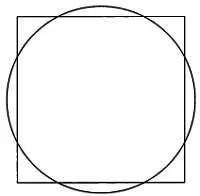
Как считают Робинс и Шут, ответ на этот вопрос заключался в том, как диаметр окружности связывался со стороной квадрата. Если соединить вершину квадрата с серединой его стороны, получится прямоугольный треугольник с гипотенузой, равной √80. Это значение весьма схоже с диаметром окружности, равным √81 = 9.

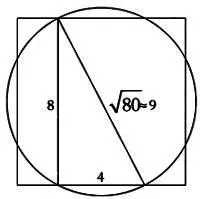
Любопытно, что если мы примем длину гипотенузы прямоугольного треугольника со сторонами 8 и 4 равной не √80, а 9, то получим еще более точное значение площади круга (64 ближе к 63,617, чем 62,83):

Неверная длина гипотенузы: 8 2= 64 кв. ед.

Точное значение: π· 4,5 2= 63,617… кв. ед.

Точная длина гипотенузы: π ·(√80/2) 2= 62,8318… кв. ед.

В любом случае ошибка будет меньше, если мы примем площадь круга диаметром 9 единиц равной 64 кв. ед., а не 63 кв. ед. (такова площадь неправильного восьмиугольника, рассмотренного ранее).

Неудивительно, что при решении этой задачи был выбран квадрат со стороной 9 единиц. Но почему именно 9? Если мы возьмем за основу квадрат со стороной в 3 единицы, то получим, что площадь восьмиугольника равна 7 кв. ед. Построить квадрат такой площади нельзя без использования иррациональных чисел. Площади квадратов со сторонами, например, 4 и 9 будут слишком далеки от реального значения. Возможно, для построения восьмиугольника египтяне брали за основу квадрат с длиной стороны, кратной 3. Но какое число, кратное 3, удобнее всего? Соотношение между площадью вписанного круга ( S о ), площадью квадрата со стороной 3 х и площадью вписанного неправильного восьмиугольника ( S 8 ) таково: