Франсиско Мартин Касальдеррей - Мир математики. Том 16. Обман чувств. Наука о перспективе

Как указано в тексте, книга «О перспективе в живописи» Пьеро делла Франче ска была переведена на латынь его другом, мастером Маттео.

Пьеро делла Франческа был не только великим художником, но и автором нескольких книг по математике: уже упомянутой «О перспективе в живописи», «Трактата об абаке» и книги по геометрии, озаглавленной «Книга о пяти правильных телах».

«Трактат об абаке», как признается в предисловии сам автор, был написан не для использования в школах абака, а по просьбе друзей, возможно живописцев, как и он сам. В остальном структура книги схожа с остальными трактатами об абаке с единственным, но очень важным отличием: геометрии уделено намного больше внимания, чем обычно. Ей посвящены 48 из 127 страниц книги. В области арифметики «Трактат об абаке» может служить примером других подобных трудов того времени. Рассмотрим в качестве примера, как объясняется правило пропорции.

«Семь локтей ткани стоят девять лир. Сколько стоит пять локтей ткани?»

Лира — монета того времени, название которой происходило от латинской меры веса libra . Флорентийская лира равнялась 20 сольдо, равных 12 денаро каждое, подобно английскому фунту стерлингов, который вплоть до реформы 1971 года равнялся 20 шиллингам, каждый из которых был равен 12 пенни. Решение задачи таково:

Разворот «Книги о пяти правильных телах» Пьеро делла Франческа.

«Нужно сделать так: умножь число, которое хочешь узнать, на то, сколько стоят семь локтей ткани, то есть 9 лир, то есть 5 на 9, что дает 45. Раздели затем результат на 7; получишь 6 лир и 3 лиры в остатке. Переведи их в сольдо и получишь 60. Раздели их на 7 и в результате получишь 8 сольдо и 4 в остатке. Переведи их в денаро, что дает 48, снова раздели на 7. Результат равняется 6 денаро и 6/7. Получишь, что 5 локтей ткани этой цены будут стоить 6 лир, 8 сольдо, 6 денаро и 6/7».

В «Книге о пяти правильных телах» приведено множество геометрических задач, заимствованных из «Трактата об абаке», которые в некоторых случаях изложены более подробно. Этот труд состоит из четырех томов. В первом, который носит вводный характер, рассматриваются плоские многоугольники, во втором и третьем — пять Платоновых тел (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр) и вписанные фигуры. В четвертом и последнем томе изучаются другие многогранники, среди которых рассматриваются шесть из тринадцати архимедовых тел, или полуправильных многогранников. Всего в книге 140 задач, в 59 из которых речь идет о правильных многогранниках. Несмотря на то что задачи в книге разделены на классы, она во многом носит новаторский характер и имеет четко организованную структуру. В ней также рассматривается одна из классических тем древнегреческой геометрии — правильные многогранники, о которых писал Евклид в «Началах» и Архимед в трудах «О шаре и цилиндре» и «О коноидах и сфероидах».

В книге представлены задачи такого типа:

«Возьмем сферическое тело диаметром 7. Хочу поместить в него фигуру с четырьмя треугольными равносторонними гранями так, чтобы каждая вершина касалась окружности [ sic ]. Чему равны ребра фигуры?»

В качестве приближенного значения π использовалась дробь 22/7. Сохранился единственный экземпляр этой книги, который находится в Ватиканской библиотеке. Это был единственный труд Пьеро делла Франческа, отпечатанный в эпоху Возрождения. Изначально он представлял собой приложение к книге Луки Пачоли «О божественной пропорции», опубликованной в Венеции в 1509 году, которая подстегнула интерес к математическому и теоретическому изучению пространственных геометрических фигур.

Изучение математики для художников перестало быть чем-то носящим чисто практический характер и стало обязательным на пути к вершинам знания.

В «Книге о пяти правильных телах» Пьеро делла Франческа рассматривает любопытную задачу, в которой нужно определить объем общей части двух цилиндров равного диаметра, пересекающихся перпендикулярно друг другу.

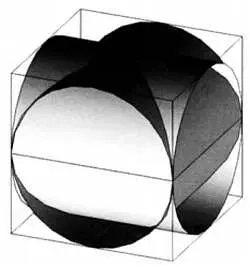
Два перпендикулярных цилиндра равного диаметра в разрезе.

(источник: FMC)

Он пытался определить объем следующей фигуры.

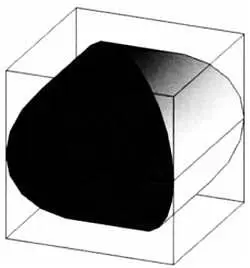
Удвоенный купольный свод.

(источник: FMC)

Пьеро делла Франческа подтвердил, что объем этого тела равен 2/3· d 3, где d — диаметр цилиндров. Более того, он посчитал необходимым объяснить, почему объем вычисляется именно по этой формуле. Подобный подход не применялся в других книгах того времени. В доказательстве использовались две следующих фигуры.

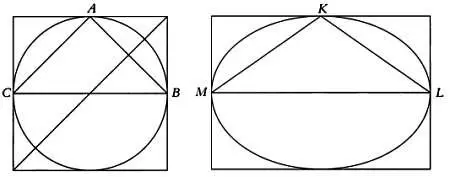
На первой иллюстрации изображен квадрат со вписанной в него окружностью, в которую вписан треугольник АВС , где ВС — диаметр окружности. На второй иллюстрации изображен прямоугольник той же высоты, что и квадрат на первом рисунке, и ширины, равной диагонали этого квадрата. В этот прямоугольник вписан эллипс, в него, в свою очередь, — треугольник KLM , где LM — большая ось эллипса. Далее Пьеро делла Франческа установил следующее соотношение:

Затем он перешел к следующим объемным фигурам.

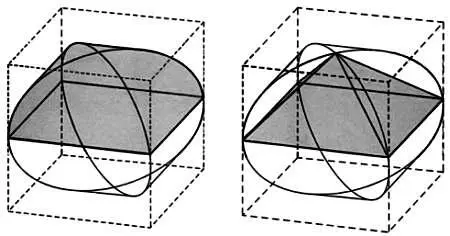
Удвоенный купольный свод и вписанная в него пирамида.

(источник: FMC)

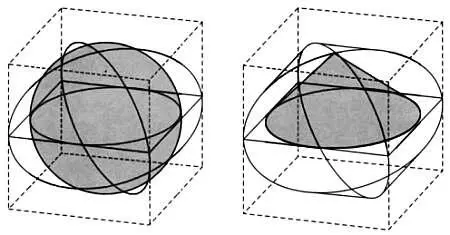
Сфера, вписанная в удвоенный купольный свод, и конус, вписанный в сферу.

(источник: FMC)

Далее без дополнительных объяснений он приводит следующее соотношение, полученное тем же способом, что и в случае с плоскими фигурами:

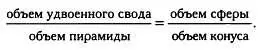
После этого он выражает объем удвоенного свода V :

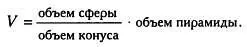
Это равносильно

Иными словами,