Пере Грима - Том13. Абсолютная точность и другие иллюзии. Секреты статистики

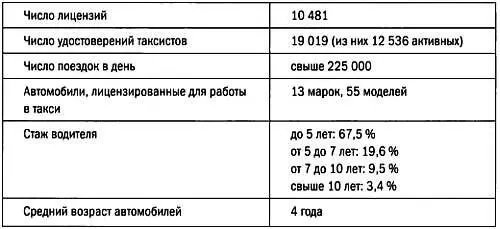
Однако если эта информация недоступна в Интернете, можно воспользоваться методами статистики. Номер лицензии написан на каждом автомобиле такси. Максимально возможным номером является число выданных лицензий. Когда мы покупаем новый автомобиль, нам выдается новый номер (следующий за последним выданным), а номер старого автомобиля уничтожается.

Однако с номером лицензии такси дело обстоит иначе (возможно, с некоторыми исключениями): число лицензий фиксировано, и если кто-то хочет приобрести ее, то может купить только у одного из ее нынешних обладателей. Номер лицензии при этом не изменится. Это значительно упрощает подсчеты. Не пользуясь ни телефоном, ни Интернетом, постояв в центре города всего 10 минут, можно очень точно определить число такси в городе. Посмотрим, как это делается.

Допустим, мы выбрали из генеральной совокупности следующие значения: 8, 14, 22, 27 и 35. Попробуем оценить число элементов генеральной совокупности на основе этой выборки. Оно будет однозначно больше 25, так как выборка содержит число 35, и крайне маловероятно, что оно будет равно 1000, так как все пять случайно выбранных элементов генеральной совокупности достаточно невелики. Точная оценка будет примерно равной 40 или 50.

Первое правило для оценки числа элементов генеральной совокупности может быть таким: общее число элементов в два раза больше среднего значения минус 1. Например, если генеральная совокупность состоит из 10 элементов 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10, то среднее значение будет равно 5,5, а общее число элементов — 2·5,5–1. Если x¯ — среднее значение генеральной совокупности из N последовательных чисел, начинающихся с 1, то всегда выполняется следующее соотношение:

N = 2 x¯ — 1

Если мы применим эту формулу к вышеприведенным данным о выборке, получим, что ее среднее значение равно 21,2, а примерное число элементов генеральной совокупности составит 2·21,2–1 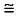41. Эта оценка очень близка к той, что мы предположили изначально.

Однако эта формула имеет один очень важный недостаток. Предположим, даны числа 3, 4, 6 и 15. Их среднее значение равно 7, а оценка общего числа элементов равна 13. Это очевидно неверно, так как выборка содержит число 15, следовательно, генеральная совокупность содержит минимум 15 элементов. Забавно, что результаты, полученные с помощью сложных методов, нередко противоречат элементарному здравому смыслу. Нужен иной способ. В действительности, чтобы определить общее число элементов совокупности в нашем примере, достаточно знать, сколько значений больше 35.

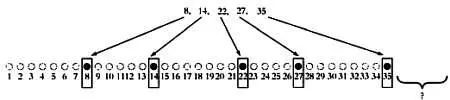
Достаточно разумный вариант — руководствуясь соображениями симметрии, предположить, что после последнего элемента находится столько же элементов, сколько перед первым. В нашем примере мы сложим 7 и 35 и получим примерное число элементов генеральной совокупности — 42. Этот метод неудобен тем, что мы не учитываем элементы, расположенные между элементами выборки. Между тем всегда следует использовать всю доступную информацию. Для этого мы добавим к последнему значению в выборке среднее расстояние между элементами выборки (первое расстояние будет равно числу элементов совокупности перед первым элементом выборки).

В нашем случае это среднее расстояние будет равно:

(7 + 5 + 7 + 4 + 7)/5 = 6

Следовательно, оценка общего числа элементов совокупности равна 41. Пусть х 1, x 2 …, х n — значения, расположенные на 1, 2, n -м местах. В этом случае среднее расстояние, которое нужно прибавить, будет вычисляться по формуле:

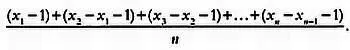
Нетрудно видеть, что эта формула равносильна следующей:

( x n / n ) — 1

Следовательно, более точную оценку общего числа элементов генеральной совокупности можно вычислить по формуле:

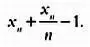
Насколько точна эта оценка? С помощью методов математической статистики можно доказать, что она является максимально точной из возможных. На языке специалистов такая оценка называется равномерно несмещенной оценкой с минимальной дисперсией.

Таким образом, нам достаточно записать номера лицензий 20 такси, прибавить к наибольшему из них его же значение, поделенное на 20, и вычесть 1. В нашем примере, если число лицензий равно 10481 и они пронумерованы последовательными числами, то в 95 % случаев оценка, выполненная по этой формуле, будет лежать в интервале от 9175 до 10990.

Очевидно, что этот метод подходит не только для подсчета числа такси в городах. Его также можно использовать, например, чтобы определить число участников массового забега, если всем им выданы последовательные номера. Службы разведки в прошлом посредством похожих методов оценивали вооружение врага. Мы знаем, что оружие имеет табельный номер, поэтому достаточно каким-то образом заполучить лишь несколько единиц, чтобы оценить общее количество оружия.

Сначала нужно уточнить определения: что мы будем считать домохозяйством и подключением к Интернету. Нет смысла производить подробные расчеты, если нам неизвестно точное значение используемых понятий.

В одном газетном заголовке утверждалось, что половину сигарет выкуривают люди с психическими расстройствами. Это звучало так, будто половина курильщиков — ненормальные, что выглядит явным преувеличением. Однако в тексте заметки под психическим расстройством понималась зависимость от какого-либо вещества, поэтому не половину, а почти все сигареты выкуривают люди, страдающие от никотиновой зависимости, следовательно, имеющие «психическое расстройство». Многие слова, которые мы произносим в повседневной жизни, неоднозначны. Одно из таких слов — «семья». Что такое семья? Муж, жена и их дети? А если вместе с ними живут бабушка и дедушка, их следует считать членами семьи? Достаточно странно определять принадлежность человека к семье по тому, в каком доме он живет. Семью можно понимать и в более широком смысле, как, например, на свадьбах, где «семья невесты» и «семья жениха» насчитывают по несколько десятков гостей.

* * *

ОЦЕНКА ВЫИГРЫШНОЙ КОМБИНАЦИИ НАЦИОНАЛЬНОЙ ЛОТЕРЕИ

Нам прекрасно известно, что все числа национальной лотереи выпадают с одинаковой вероятностью. Но что можно сказать о среднем значении чисел выигрышной комбинации? 7 января 2010 года выигрышная комбинация испанской национальной лотереи состояла из следующих чисел: 19, 24, 25, 38, 43 и 49, их среднее значение равно 33. В субботу, 9 января, выпали числа 13, 26, 29, 30, 31 и 43; их округленное среднее значение равно 29. Все ли средние значения выпадают с одинаковой вероятностью или некоторые из них встречаются чаще, чем другие?