Алексей Макарушин - Парадоксы эволюции. Как наличие ресурсов и отсутствие внешних угроз приводит к самоуничтожению вида и что мы можем с этим сделать

В третьей главе на отдельных примерах были кратко рассмотрены квантовые и энтропийные основания базовых энергетических предпосылок жизни и сопутствующая им диссипативность, то есть «набор свойств открытой, неравновесной, рассеивающей энергию системы, движимой градиентом энергии, что увеличивает энтропию окружающей среды». Несомненно, что физические, в первую очередь термодинамические основания, второе начало термодинамики являются наиболее всеобъемлющим оправданием существования всего живого с его общим движением к нарастанию энтропии, но с неизбежным возникновением локальных и преходящих ее снижений (флуктуаций), то есть упорядочиваний хаоса. Рассмотрение энтропии как чистой «меры беспорядка» может запутать: очевидно, что энтропия «покоящейся» системы – ровного песка в пустыне, сбалансированной группы клеток, стагнирующего человеческого общества – гораздо выше, соответственно, энтропии осыпающегося бархана, смеси клеток хозяев и клеток новых паразитов, общества в состоянии революции и гражданской войны, ввиду того, что совокупность или возможность «выбора» доступных состояний для каждой единицы или вариантов совокупностей микросостояний в «спокойной» системе гораздо больше возможностей выбора в состоянии «революции».

Так, лидер партии «Яблоко» Григорий Явлинский в своей статье «Политическая энтропия. Цифровые технологии и глобализация беспорядка» (2020) предполагает, что на смену эпохи глобализации, предположительно, более упорядоченной, приходит «век беспорядка», где «существует множество труднопредсказуемых событий и развилок, и куда, как говорится, кривая выведет, не знает никто». И этот переход с ростом беспорядка предполагается рассматривать как рост «политической энтропии». Однако более правильным будет скорее обратное – падение энтропии: несмотря на возникновение потоков событий с непредсказуемой динамикой, для отдельных людей – совокупности элементов системы – количество вариантов выбора («свободы») на самом деле уменьшается, о чем совершенно справедливо указывает и сам Г. Явлинский в заключение своей статьи, связывая это в первую очередь с добровольным отказом людей от свободы выбора, нежели направленной деятельностью авторитарных лидеров. Отдельный большой вопрос, разумеется, насколько этот выбор на самом деле доброволен, но несомненно, что само уменьшение свободы выбора для подавляющего большинства элементов системы – это несомненно снижение ее энтропии. Тем более актуальное в свете взрывного развития информационных технологий и роста все более детализированной информации о системе. Информации, к сожалению, неравномерно распределяемой, но в итоге дающей уменьшение неполноты информации о системе (см. ниже), что также показывает скорее падение «политической энтропии», нежели ее возрастание. И тем более, что «добровольный отказ от свободы» и рост информационной насыщенности общественного пространства могут оказаться двумя сторонами одной медали.

Со времен установления принципа Людвига Больцмана (ок. 1875 г.) стало возможным рассматривать классическую термодинамическую и информационную энтропию как практически и теоретически очень близкие, если не равнозначные. В формулировке Макса Планка (ок. 1900 г.) этот принцип как связь средней энтропии системы с вероятностью данного состояния определяется логарифмической зависимостью:

S = k ln(Ω),

где S – общая энтропия состояния системы, константа k = = 1,38*10-23 Дж/К, названная Планком постоянной Больцмана, а Ω – статистический вес состояния, являющийся числом возможных равновероятных микросостояний (способов), с помощью которых можно составить данное макроскопическое состояние. Более ранняя формулировка Джозайя Гиббса (1878 г.) для микросостояний, имеющих разную вероятность, устанавливает зависимость в виде суммы произведения вероятности состояний на натуральные логарифмы этих же вероятностей, взятой с противоположным знаком:

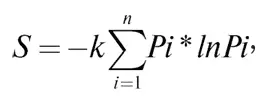
где P i – вероятность пребывания системы в состоянии i . Минус в начале формулы необходим для приведения обеих частей формулы к общему знаку из-за постоянной отрицательности логарифмов вероятности (так как вероятности всегда меньше 1) и неизменной положительности энтропии. Сам Больцман, комментируя свое физико-статистическое определение энтропии, отмечал, что энтропия характеризует недостающую информацию о системе. В этой интерпретации энтропия может считаться мерой неполноты информации о системе.

В ходе разработки углубленной теории информации информационной энтропией стала считаться мера неопределенности, независимо выведенная как сумма произведений вероятностей событий на логарифмы этих же вероятностей (формула Хартли-Шеннона, основателей теории информации), взятая с противоположным знаком:

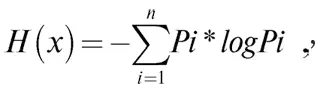
где H ( x ) – средняя энтропия сообщения, иногда обозначаемая также как мера неопределенности какого-либо события, или даже как количество информации, P i – вероятность отдельного события i. Основание логарифма в принципе может быть любым больше 1: в двоичных информационных системах – 2, математические статистики, использующие формулу в различных научных дисциплинах, в том числе биологических и клинических, часто используют натуральный логарифм.

Отрицательная энтропия, которую описывал Эрвин Шредингер, это, разумеется, не энтропия с отрицательным знаком – это, очень условно говоря, мера удаленности от максимальной энтропии в рассматриваемой системе, хотя само понятие негативной энтропии (негэнтропии) на самом деле гораздо более сложное, глубокое и весьма запутанное, даже в сравнении с часто неоднозначно понимаемой «обычной», «позитивной» энтропией в своих самых разнообразных интерпретациях. Некоторые исследователи, вслед за Норбертом Винером, увидевшим за очевидным сходством формул Больцмана-Гиббса и Хартли-Шеннона более глубокую связь термодинамической и информационной энтропий, ассоциируют негэнтропию с информацией, что представляется красивым, но до сих пор далеко не всеми признаваемым суждением.

Одной из точек смыкания термодинамической и информационной энтропии являлся, например, известный парадокс «демона Максвелла», гипотетического устройства, стоящего на границе двух объемов и способного различать быстрые и медленные молекулы и, соответственно, пропускать или не пропускать молекулы в одну сторону, что спонтанно ведет к увеличению упорядоченности системы и падению энтропии, что формально противоречит второму началу термодинамики. Решение парадокса было предложено французским и американским физиком Леоном Бриллюэном, математически показавшем, что даже демон ничего не хочет делать бесплатно: чтобы увидеть скорость молекулы, ему нужно заплатить энергией, которая не может быть менее энергии одного теплового кванта (0,025 эВ при комнатной температуре), и эта энергия соответствует минимальной цене одного бита информации. То есть демон совершает работу по обработке информации, и эта работа охлаждает одно тело и нагревает другое, и так же, как за работу любого домашнего холодильника, за эту работу надо платить.