Рене Декарт - Сомневайся во всем. С комментариями и иллюстрациями

А именно, когда мы узнаем какую-либо величину благодаря тому, что нам даны части, составляющие ее, то мы пользуемся сложением. Когда мы узнаем часть благодаря тому, что нам дано целое и превышение целого над этой частью, то такое действие будет вычитанием; и нет иных способов выведения одной величины из других величин, взятых в абсолютном смысле, в которых она содержится как бы то ни было. Но если какая-либо величина находится между другими, от которых она совершенно отлична и которые ее совсем не содержат в себе, то ее необходимо поставить в какое-либо отношение к последним. Это отношение, или соотношение, если его нужно отыскивать прямо, можно найти путем умножения, а если его нужно отыскивать косвенно, то путем деления.

Для лучшего уразумения этих двух пунктов нужно понять, что единица, о которой мы уже говорили, является здесь принципом, или основой, всех отношений и что в ряде последовательно пропорциональных величин она занимает первую ступень, данные величины – вторую, искомые – третью, четвертую и все остальные, если отношение оказывается прямым; если же оно косвенное, то искомая величина занимает вторую ступень и другие промежуточные, а данная величина – последнюю.

Ибо когда говорится, что единица относится к а или к данному числу 5 так же, как b или данное число 7 относится к искомому ab или 35, то а и b в этом случае находятся на второй ступени, произведение же их ab – на третьей. То же самое, когда добавляют: единица относится к с или 9 так же, как ab или 35 относятся к искомому abc или 315, в этом случае abc находятся на четвертой ступени, будучи произведением двойного умножения ab на с, величин, находящихся на второй ступени, и т. д. Подобно этому: как единица относится к а <���или> 5, так же и а <���или> 5 относится к а 2или 25; или еще: как единица относится к а <���или> 5, так же и а 2<���или> 25 относится к а 3<���или> 125; или, наконец: как единица относится к а или 5, так же и а 3или 125 относится к а 4, т. е. к 625, и т. д. Конечно, действие умножения производится одинаково, умножается ли величина на самое себя или на какую-нибудь совсем другую величину.

В случае же, если говорится: как единица относится к а или 5 к данному делителю, так же В или 7, искомое число, относится к ab или 35, данному делимому, то здесь порядок смешанный и непрямой, вследствие чего искомое В не может быть найдено иначе, как путем деления данного ab на а – тоже данное. То же самое, когда говорится: как единица относится к А или искомому числу 5, так же и А или 5 искомое относится к а 2или 25 данному. Или еще: как единица относится к А <���или> 5 искомому, так же и А 2или 25 искомое относится к а 3или 125 данному и т. д. Мы объединяем все эти действия под названием деления, хотя и нужно заметить, что два последних вида заключают в себе больше трудностей, чем первые, потому что в них искомая величина встречается чаще и, следовательно, имеет больше отношений. Смысл этих примеров тот же самый, как если бы говорилось, что нужно извлечь квадратный корень из а 2(или) 25 или кубичный из а 3или 125 и т. д. Такой способ выражения, употребительный среди счетчиков, является равнозначным – пользуясь также термином геометров – выражением, обозначающим действие отыскания средней пропорциональной между наперед взятой величиной, называемой нами единицей, и той, которая обозначается а 2, или двух среднепропорциональных между единицей и а 3и т. д.

Отсюда нетрудно сделать вывод, почему эти два действия удовлетворяют в отыскании любых величин, которые должны выводиться из других величин по тому или иному отношению. Уразумев это, нам остается объяснить, как эти действия должны быть представлены рассмотрению воображения и как их нужно сделать наглядными, для того чтобы затем объяснить их употребление или обращение с ними.

Если нам нужно произвести сложение или вычитание, то мы будем представлять предмет в виде линии или величины, обладающей протяжением, в которой нужно рассматривать только длину, так как если нужно прибавить линию а к линии b , то мы соединим их друг с другом таким образом: аb

и получим сумму c.

Если же, наоборот, нужно вычесть меньшую величину из большей, т. е.

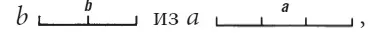
то мы наложим их одну на другую таким образом:

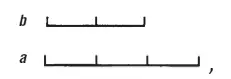
и получим часть большей, которая не может быть прикрыта меньшей, а именно:

В умножении мы будем представлять данные величины тоже в виде линий, но вообразим, что они составляют прямоугольник. Если мы умножаем а 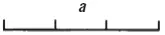на b 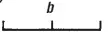, то поставим их в виде прямого угла

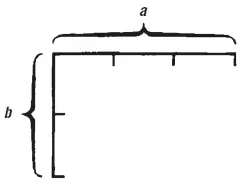
и получим прямоугольник

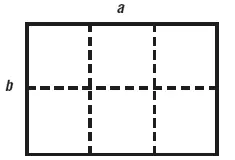
С другой стороны, если мы хотим умножить аb на с

то аb нужно представлять в виде такой же линии аb

и мы получим для аbс:

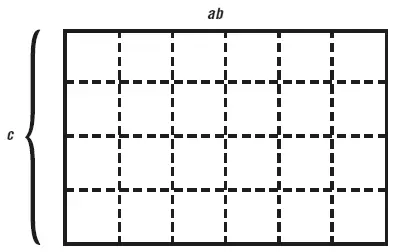
Наконец, при делении, где дан делитель, мы будем воображать делимую величину в виде прямоугольника, одна сторона которого делитель, а другая – частное. Так, например, если прямоугольник аb требуется разделить на а,