Николай Кузанский - Сочинения в 2-х томах. Том 1

Действуя так и приступая к делу под водительством максимальной истины, вспомним сначала разные высказывания святых мужей и высочайших умов, занимавшихся математическими фигурами. Благочестивый Ансельм сравнивал максимальную истину с бесконечной прямизной [55] Ансельм Кентерберийский. Диал. об истине 10-11. ; следуя ему, мы обращаемся к фигуре прямизны, которую я изображаю в виде прямой линии. Другие многоопытные мужи сравнивали преблагословенную Троицу с треугольником о трех равных прямых углах [56] Ксенократ (фр. 23 по Хейнце), Прокл (Коммент. на I кн. Евклидовых «Начал» 168,14 по Фридлейну), Пселл («О действии демонов» 11) уподобляли божество равностороннему треугольнику, но треугольник о трех равных прямых углах до Николая неизвестен. ; поскольку он, как будет показано, обязательно должен иметь бесконечные стороны, его можно назвать бесконечным треугольником. Мы следуем и за, ними. Третьи, пытаясь представить в математической фигуре бесконечное единство, называли Бога бесконечным кругом. А созерцатели всецело актуального божественного бытия называли Бога как бы бесконечным шаром [57] Сравнения бога с кругом и шаром есть у Генриха Сузо («Житие» 51), в «Песни о Троице» анонимного немецкого мистика, у Экхарта со ссылкой на Гермеса Трисмегиста. . Опять-таки, мы покажем, что и они правильно понимали величайший максимум и что смысл у них всех один.

Итак, я утверждаю, что если бы существовала бесконечная линия, она была бы прямой, она была бы треугольником, она была бы кругом, и она была бы шаром; равным образом, если бы существовал бесконечный шар, он был бы кругом, треугольником и линией; и то же самое надо говорить о бесконечном треугольнике и бесконечном круге.

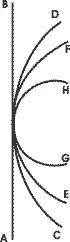
Во-первых, что бесконечная линия будет прямой, очевидно: диаметр круга есть прямая линия, а окружность — кривая линия, большая диаметра; если эта кривая тем меньше в своей кривизне, чем большего круга окружностью она является, то окружность максимального круга, больше которого не может быть, минимально крива, а стало быть, максимально пряма. Минимум совпадает таким образом с максимумом. Даже и на глаз видно, что максимальная линия с необходимостью максимально пряма и минимально крива. Здесь не может оставаться ни тени сомнения, когда мы рас смотрим на фигуре сбоку, что дуга CD большего круга больше отступает от кривизны, чем дуга EF меньшего круга, а та больше отходит от кривизны, чем дуга GH еще меньшего круга, почему прямая линия AB будет дугой максимального круга, который уже не может увеличиться. Так мы видим, что максимальная и бесконечная линия по необходимости совершенно прямая и кривизна ей не противоположна; мало того, кривизна в этой максимальной линии есть прямизна. Это первое, что требовалось доказать.

Во-вторых, как сказано, бесконечная линия есть максимальный треугольник, круг и шар. Для доказательства этого надо рассмотреть на конечных линиях, что заключено в возможности конечной линии; поскольку все, чем конечная линия является в возможности, бесконечная линия есть в действительности, мы сможем увидеть искомое еще яснее.

Мы знаем прежде всего, что конечная линия по своей длине может быть длиннее и прямее; а уже доказано, что максимальная линия — самая длинная и прямая. Потом, если линия AB будет обведена вокруг неподвижной точки А, пока не придет в С, возникнет треугольник. Если вращение будет совершаться, пока В по придет в свое начальное положение, возникнет круг.

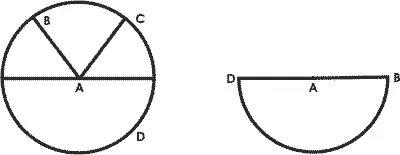
Опять-таки, если В будет обведено вокруг неподвижного А до точки, противоположной своему начальному положению, то есть до D, то из линий AB и AD образуется одна непрерывная линия и будет описан полукруг. Наконец, если этот полукруг будет обведен вокруг неподвижного диаметра BD, то получится шар. И этот шар — последняя возможность линии, целиком переходящей в нем в действительность, потому что шар уже не заключает в себе возможности никакой последующей фигуры.

Поскольку, таким образом, в возможности конечной линии заключены все эти фигуры, а бесконечная линия есть действительным образом все то, возможность чего представляет конечная, то, следовательно, бесконечная линия есть и треугольник, и круг, и шар, что и следовало доказать.

Так как ты, наверное, захочешь яснее убедиться, что бесконечное есть действительность всего, что заключено в возможности конечного, дам тебе совершенно удостовериться в этом.

Воображение, неспособное выйти за пределы чувственных вещей, не улавливает, что линия может быть треугольником, потому что количественное различие обоих несоизмеримо; но для разума это нетрудно.

В самом деле, уже доказано, что максимальным и бесконечным может быть только одно. Ясно также, раз всякие две стороны любого треугольника в сумме не могут быть меньше третьей, что если у треугольника одна из сторон бесконечна, две другие будут не меньше. Потом, поскольку любая часть бесконечности бесконечна, у треугольника с одной бесконечной стороной другие тоже обязательно будут бесконечными. Но нескольких бесконечностей не бывает, и за пределами воображения ты трансцендентно понимаешь, что бесконечный треугольник не может состоять из нескольких линий, хоть этот максимальный, не составной и простейший треугольник есть истиннейший треугольник, обязательно имеющий три линии, и, значит, единственная бесконечная линия с необходимостью оказывается в нем тремя, а три — одной, простейшей. То же в отношении углов: в нем будет только один бесконечный угол, и этот угол — три угла, а три угла — один. Не будет этот максимальный треугольник и состоять из сторон и углов, но бесконечная линия и угол в нем — одно и то же, так что линия есть и угол, раз весь треугольник — линия.

Понять это тебе поможет еще восхождение от количественного треугольника к не-количественному (nоnquantum). Всякий количественный треугольник, как известно, имеет три угла, равные двум прямым, и чем больше один угол, тем меньше другие. Хотя каждый угол треугольника может увеличиваться только до двух прямых исключительно, а не максимально, в соответствии с нашим первым принципом, однако допустим, что он увеличивается максимально до двух прямых включительно, оставаясь при этом треугольником. Тогда, окажется, что у треугольника один угол, который есть три, и три образуют один. Точно так же ты сможешь убедиться, что треугольник есть линия. Любые две стороны количественного треугольника в сумме настолько длиннее третьей, насколько образуемый ими угол меньше двух прямых; например, поскольку угол ВАС много меньше двух прямых, линии BA и АC в сумме много длиннее ВС. Значит, чем больше этот угол, например угол ВDС, тем меньше линии BD и DC превышают линию ВС и тем меньше поверхность.