Герман Хакен - Тайны природы. Синергетика: учение о взаимодействии

Другой мобиль послужит нам иллюстрацией отношения «или». По сути дела, это будет практически тот же механизм, что описан в предыдущем примере, с той лишь разницей, что сливное отверстие в переливном баке расположено на этот раз у самого его дна, что означает возможность наполнения нижней емкости даже в том случае, когда в переливной бак попадает вода только из одного из верхних сосудов, т. е. нижняя емкость наполняется водой, если наполнить хотя бы один из верхних сосудов (рис. 17.14, 17.15).

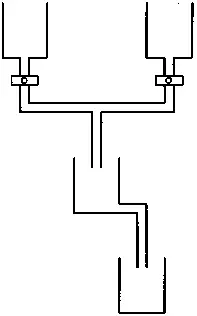
Рис. 17.14. Схема реализации логической операции «или». Для наполнения находящегося снизу сосуда необходимо наполнить хотя бы один из верхних сосудов

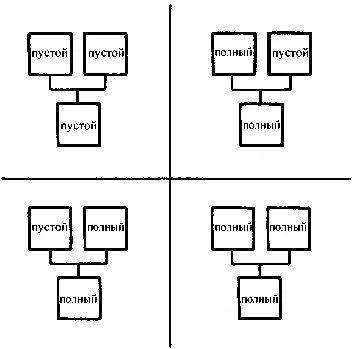
Рис. 17.15. Возможные варианты наполнения сосудов, изображенных на рис. 17.14

Как показывает математическая логика, все логические операции можно представить в виде цепочек таких простейших шагов, как «и», «или», «да», «нет». Однако не будем останавливаться на слишком уж абстрактных предметах; посмотрим, каким же образом эти логические операции могут быть приспособлены к практическим вычислениям, т. е. к численным расчетам. Для этого нам придется забраться «внутрь» компьютера и исследовать все его тайны и чудеса непосредственно на месте.

Математики утверждают, что все числа могут быть выражены посредством различных комбинаций нулей и единиц (в так называемой двоичной системе счисления). Кроме того, различные математические операции — такие, как сложение, вычитание, умножение и деление — над числами, представленными в этой двоичной системе, производятся по тем же правилам, что знакомы нам по привычной, десятичной системе счисления.

Это может показаться странным, но отдельные компоненты компьютера «общаются» друг с другом именно на таком примитивном языке; компьютерные сигналы состоят лишь из нулей и единиц. Воспользуемся примером логической операции «и» для того, чтобы понять, каким образом компьютер оказывается способен перемножить числа «1» и «0», и убедиться в том, что он делает это правильно. Иными словами, проверим, получит ли машина тот же результат, что и мы. Каждый школьник знает, что 0×0 = 0, 0×1 = 0, 1×0 = 0 и 1×1 = 1. Все четыре решения можно в точности воспроизвести с помощью нашего мобиля, своего рода «водяного компьютера». Пустой сосуд при этом будет обозначать нуль, а полный — единицу. Если оба верхних сосуда пусты, то пуст оказывается и нижний, соответствующий конечному результату (который равен нулю). Таким образом, произведение 0×0 = 0 машина вычисляет верно. Если один из верхних сосудов наполнен водой, а второй пуст, то нижний сосуд оказывается пуст; следовательно, подтверждается и верность решения 0×1=0 или 1×0 = 0. Если же полны оба верхних сосуда, то и нижний сосуд в конечном итоге тоже окажется полон: 1×1 = 1. Таким образом, с таблицей умножения, которой пользуется компьютер, похоже, все в порядке.

Остальные арифметические действия также можно воспроизвести с помощью водяного мобиля. Интересующимся читателям на рис. 17.16 предлагается рассмотреть процесс сложения, который, правда, требует применения несколько более сложной конструкции мобиля. На примере устройств, подобных показанным здесь, мы можем легко убедиться в том, что компьютер осуществляет все вычислительные операции при помощи весьма несложных устройств.

Идея привлечения в качестве иллюстраций такого рода «каскадов» может показаться слегка притянутой за уши. Однако в некоторых компаниях, занимающихся производством вычислительной техники, вам и в самом деле могут продемонстрировать рабочие модели компьютеров в виде аналогичных описанным гидравлических устройств.

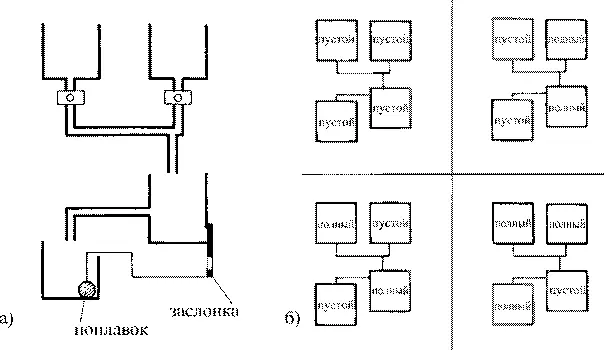
Рис. 17.16. Мобиль для сложения. Слева (а) показано устройство мобиля, с помощью которого можно воспроизвести операцию сложения. В зависимости от того, полна или пуста верхняя емкость, она представляет число 1 или 0. Наполнение нижних емкостей демонстрирует результат сложения в двоичной (бинарной) системе счисления. В дальнейшем мы будем говорить только о нижних емкостях. Случай, когда обе емкости остаются пустыми, соответствует конечному результату, равному нулю. Если левая емкость пуста, а правая — наполнена водой, это означает 1. Если же наполнена левая емкость, а пуста правая, то такой результат записывается в двоичной системе счисления как 10, что в десятичной системе соответствует числу 2. На схемах справа (b) поясняются все возможные варианты производимого сложения. Случай, когда обе верхние емкости пусты, соответствует сложению двух нулей. Естественно, обе нижние емкости в данном случае остаются пустыми. Если же открыть оба крана, когда левая верхняя емкость пуста, а правая наполнена водой, то правая нижняя емкость наполнится, но левая останется пустой. Этот результат будет соответствовать значению суммы 1. Аналогичное рассуждение применимо, естественно, и к случаю, когда полна левая верхняя емкость, а пуста правая. Особенно интересен случай, соответствующий сложению двух единиц; обе верхние емкости при этом наполнены водой. Открыв кран под одним из верхних сосудов, мы наполним водой сначала только правую нижнюю емкость. При добавлении в нее воды из второго верхнего сосуда происходит наполнение и левой нижней емкости. В этот момент, благодаря поплавку, поднимается заслонка в правой нижней емкости, выпуская из нее всю воду; такой конечный результат, показанный на схеме внизу справа, соответствует 10 в двоичной системе (или 2 в десятичной). Как можно убедиться, представленное устройство действительно способно производить сложение в двоичной системе счисления. Соответствующие комбинации подобных устройств позволяют складывать числа и более сложные, нежели 0 или 1; однако принцип, лежащий в основе процесса, остается по сути своей неизменным

Схемы на рис. 17.16 дают представление о том, что уже такая простая операция как «и» требует довольно сложной системы труб. Труб же, необходимых для выполнения такими компьютерами более сложных вычислительных операций (например умножения или деления), запросто хватило бы на целый многоэтажный дом. Отсюда совершенно естественно возникает вопрос, адресованный физикам или инженерам-электрикам: нельзя ли создать схемы соединений, подобных описанным, но меньших размеров? А раз в таких схемах необходимо задействовать огромное количество элементов — что, как нетрудно видеть, подразумевает огромное количество отдельных операций, — следует в то же время стремиться и к тому, чтобы сократить длительность каждой операции. К счастью, физикам давно известны иные способы создания подобных схем, не нуждающиеся ни в воде, ни в трубах. В самом начале этой книги мы уже говорили об электронах — мельчайших частицах, движение которых создает в металлическом проводнике электрический ток. Электроны способны не только переносить электрический заряд, но и сохранять его, как это происходит, скажем, в батареях или конденсаторах.