Павел Новиков - Полное собрание сочинений. Том 4

Что значит «прямая непрерывна»? Это значит, что вся она состоит из бесконечного числа точек бесконечно малого размера. Говоря относительно количества, мы тем самым утверждаем, что вся она состоит из чисел с бесконечным количеством знаков после запятой. Говоря о бытии, таким образом, предполагается, что такой подход не абстрактный (чисто математический), а имеет место быть в самой организации природы. Далее мы можем пойти двумя путями. Первый – древний (рис. 1): где, t – время; х – событие.

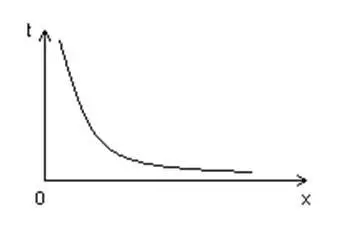
Рис. 1

Так событие никогда не наступит, никакая вещь полностью не изменится, ибо до события всегда будет 0,0…01 с, 0,0…001 с; 0,0…0001 с и т.д. В общем, сие – известная апория Зенона. Конечно, жутко хочется обозвать всё это софизмом (не нравится, а сказать нечего софизм), но никакой софистики здесь нет; всё в пределах действия законов логики и без нарушения оных. А задачка не решается. Если, конечно, не применить дискретность. Если же мы применяем дискретный подход, то проблема сразу же снимается. Вышеприведённый график будет выглядеть уже следующим образом (рис. 2):

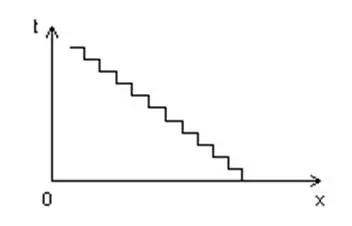
Рис. 2

Это означает, что время дискретно. Если время имеет непрерывный характер, никакое взаимодействие не может не только начаться, но и завершиться. Т.е., невозможно никакое взаимодействие и изменение; неподвижный, мёртвый мир. Однако ж практика (хоть даже и только внутренняя) говорит нам совсем иное. Но то, конечно, лишь время и ничего более. Мы же пойдём дальше.

Бесконечность есть понятие сугубо математическое и сугубо абстрактное. По крайней мере, эмпирически её ещё никто не видел. Бесконечность двояка: бесконечно большая величина и бесконечно малая . Нам будет интересен именно второй вид. Бесконечно малые величины имеют ту особенность, что с ними невозможно проводить арифметические действия. Если сложить десять бесконечно малых величин, то единица не получится, получается та же бесконечно малая величина. Но коли уж мы говорим, что бесконечность (бесконечно малые значения) существуют реально, то давайте перефразируем прошлый пример по отношению к самой действительности: если сложить десять бесконечно малых расстояний, миллиметра не получится. Однако, в мире мы отчётливо видим и миллиметры, и килограммы, и Джоули. Следовательно, из бесконечно малых величин они не могут состоять в принципе, ибо тогда ничего бы не было (а оно, чёрт побери, есть!). Если вам не по душе такое умозрительное доказательство дискретности, пожалуйста, вот вам наука. По Гейзенбергу, чем меньше пространства занимает частица, тем больше её полная масса. Отсюда, если пространство, занимаемое частицей, бесконечно мало, то и её масса бесконечно велика. Сами понимаете, такое актуальное положение вещей есть глупость. И если в природе нет величин бесконечно малых, то, значит, есть величины малые конечно. Например, минимальная длина 0,1 мм, тогда из десяти минимальных длин мы получаем тот самый стоящий перед нашими глазами миллиметр. Только так (через конечность) можно оправдать вообще наличие бытия.

Таким образом, в данном примере не может быть расстояния меньше 0,1 мм . После этого 0,1 сразу же следует ноль. Точно так же с большими расстояниями. Может быть 12,1 мм, 12,2 мм, но не может быть 12,15 или 12,18 мм. Если этот ряд продолжать до бесконечности (12,189573… мм), то, следовательно, потенциально существует расстояние 0,089673… мм, что, как мы установили, невозможно. Другими словами, последнее число (здесь) предполагает наличие расстояния в 0,000003 мм (и так до бесконечности), т.е. мы получаем, в конце концов, то же самое бесконечно малое число, которое, как уже было сказано, в природе существовать не может . Отсюда вывод: любая величина имеет конечное количество знаков после запятой вплоть до порядка наименьшей величины . Или: всякое значение кратно наименьшему.

Примером здесь может служить тот же электрический заряд. Не бывает заряда менее 1,6х10 -19Кл (само собой, я округляю, ну да не в том дело); либо так, либо ноль. И все большие заряды обязательно кратны данному. Возможен заряд в 8х10 -18Кл, но невозможен 7,9х10 -18Кл. Это хотя и частность, но суть, я полагаю, стала более прозрачной. Если же вам неясен ход моей мысли, перечитайте , ибо очень уж это примечательно и важно.

Что нам дают такие выводы? Сама метрология говорит, что абсолютно точно можно подсчитать только количество (пять яблок, десять ложек…). И если всё в этом бытии дискретно (а иначе никакого бытия и не было бы ), то в любом изменении мы имеем дело с количественным подсчётом, который (см. мудрость метрологии) теоретически может быть абсолютно точным . Хотя, и этого пока нельзя отрицать, ещё возможны флуктуации этих самых «дискрет». Но об этом позже.

Просто? Так просто, что аж смешно! Банальность: всё, что существует, имеет свою основу, т.е. последнее, наименьшее значение, менее которого (на то оно и наименьшее) ничего быть не может. Это перечёркивает непрерывность и проявляет нам дискретность мироздания. Если вы полагаете, что такое положение несущественно – вы жестоко ошибаетесь. Дискретность означает, что существует последняя микрочастица, которая ни на что не делится, что время есть смена кадров, что… Хотя здесь, конечно, возникают новые вопросы, не менее интересные, чем в случае бесконечности: почему эта величина не делится? Из чего она состоит, если меньше нее ничего нет? Почему кадры (время) меняются именно с такой частотой, и можно ли её изменить? И т.д. Но всё это вопросы уже скорее научные, чем чисто философские, а уж тем более частные, а потому оставим их без внимания; не о том сейчас речь. Дискретность мироздания логически очевидна, со всеми вытекающими отсюда выводами. Одно удивляет: почему концепциями дискретности так мало занимаются? Нехорошо.

Детерминизм

Можем ли мы на основании дискретности говорить о познаваемости «вещи-в-себе»? С одной стороны – да. Действительно, если всё дело лишь в количестве, и количество это конечно, то мы можем абсолютно точно подсчитать что угодно, правда, пока лишь только в статике. Если же дело коснётся тех или иных преобразований, то кто сказал, что эти «дискреты» не будут флуктуировать? Если числа конечны, всё же может быть и так, что расстояние Х равно 100±5 минимальных длин. И это «+5», очевидно, может привести не только к неверному выводу (для нас), но и изменить вообще весь ход развития какого-либо процесса. В таком случае, ни о каком абсолютном знании и речи идти не может. Но можем ли мы свести на нет такую погрешность и, наконец, с полной уверенностью удариться в гносеологический оптимизм? Вы, конечно, удивитесь, но я скажу – да. Но это «да» возможно только в том случае, если все процессы в этом мире детерминированы . При этом под детерминированным я понимаю такой процесс, в котором нет места никакой случайности. В том числе необусловленному ничем отклонению или взаимодействию (это к вышеозначенному примеру «+5»). Если же абсолютной детерминации нет, то, как ни крути, мы никогда не сможем узнать Последнюю Истину; всегда будет вероятность неких отклонений: флуктуирует, флуктуирует, потом как ударится в бифуркацию и весь аттрактор насмарку! Обидно? Ну да не расстраивайтесь, это всё пустобрёхство; детерминизм спасёт мир.