Артур Шопенгауэр - О четверояком корне закона достаточного основания

Ибо если сторона ag не равна стороне ab, то одна из них больше другой. Отнимем от большей стороны ab отрезок db, равный меньшей линии ag, и проведем линию dg. Так как (в треугольниках dbg, abg) db равна ag, a bg принадлежит обеим, то две стороны db и bg равны двум сторонам ag и gb, взятым в отдельности, угод dbg равен углу agb, основная линия dg равна основной линии: ab, и треугольник abg равен треугольнику dbg, больший меньшему, что бессмысленно, следовательно, ab не неравна ag, следовательно, равна.

В этом доказательстве мы имеем основание познания истинности: теоремы. Но кто же основывает свою уверенность в этой геометрической истине на подобном доказательстве, а не на познанном созерцанием основании бытия, по которому (в силу необходимости, не допускающей дальнейшего доказательства, а доступной только созерцанию), если из обоих конечных точек линии исходят две другие линии и равномерно наклоняются друг к другу, они могут встретиться только в одной точке, находящейся на одинаковом: расстоянии от обеих конечных точек, потому что два возникающих угла составляют, собственно, только один угол, кажущийся двумя углами только из–за противоположного положения; поэтому нет основания, чтобы линии встретились ближе к одной точке, чем к другой.

Познавая основание бытия, мы выводим как необходимое следствие, обусловленное его условием, в данном случае — равенство сторон из равенства углов,— их связь; основание же познания дает нам только совместное бытие обоих. Более того, можно даже утверждать, что обычный метод доказательства убеждает нас, собственно, лишь в том, что оба равенства выступают в данной, принятой в доказательстве фигуре, а отнюдь не в том, что они всегда выступают вместе; в этой истине (поскольку необходимая связь не показана) мы обретаем только уверенность, основанную на индукции, и покоится наше убеждение на том, что это обнаруживается в каждой фигуре, построенной нами. Правда, столь легко основание бытия бросается в глаза только в таких простых теоремах, как шестая теорема Евклида; однако я убежден, что в каждой, даже самой запутанной, теореме его можно выявить и свести достоверность теоремы к такому простому созерцанию. К тому же каждый a priori сознает необходимость такого основания бытия для каждого пространственного отношения, подобно необходимости причины для каждого изменения. Конечно, обнаружить такое основание в сложных теоремах очень трудно, а здесь не место проводить сложные геометрические исследования. Поэтому только для того, чтобы еще больше уяснить свою мысль, я сведу к основанию бытия не очень сложную теорему, в которой, однако, это основание не сразу бросается в глаза.

Пропускаю десять теорем и перехожу к шестнадцатой: «В каждом треугольнике, одна сторона которого продолжена, внешний угол больше, чем каждый из двух противостоящих ему внутренних». Доказательство Евклида таково (см. рис. 4).

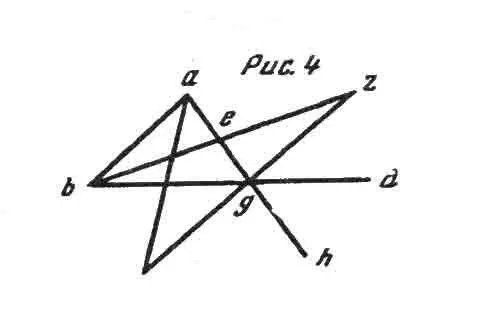
Возьмем треугольник abg, продолжим сторону bg к d, и я утверждаю, что внешний угол agd больше, чем каждый из двух противостоящих ему внутренних. Разделим сторону ag пополам в точке е, проведем линию be, продолжим ее до z p сделаем ez равной еb, соединим точки z и g и продолжим ag до h. Так как ае равна eg и be равна ez, то две стороны ае и eb равны двум сторонам ge и ez, взятым в отдельности, и угол aeb равен углу zeg, ибо это — вертикальные углы. Тем самым основная линия ab равна основной линии zg и треугольник аbe равен треугольнику zeg: а остальные углы равны остальным углам, следовательно, и угол bae равен углу egz. Однако угол egd больше угла egz, следовательно, и угол agd больше угла bae. Если разделить пополам и линию bg, то подобным же образом можно доказать, что угол bgh, т. е. его вертикальный угол agd, больше, чем abg.

Я бы доказал эту теорему следующим образом (см. рис. 5). Для того чтобы угол bag был равен, а тем более превзошел бы, угол agd, линия ba (ибо это и означает равенство углов) должна была бы находиться по отношению к линии ga в том же направлении, как bd, т. е. быть параллельной bd, другими словами, никогда не пересекаться с bd; однако для того чтобы образовать треугольник, она должна (основание бытия) пересечься с bd, т. е. совершить противоположное требуемому для того, чтобы угол bag хотя бы достиг величины угла agd.

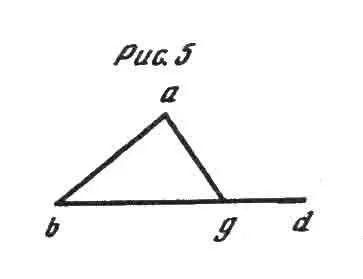
Для того чтобы угол abd был равен углу agd, а тем более превосходил его (ибо именно это и означает равенство углов), линия bа должна была бы находиться по отношению к линии ga в том же направлении, что bd, т. е. идти параллельно bd, другими словами, никогда не пересекаться с ней; но для того чтобы образовать треугольник (основание бытия), она должна пересечься с линией ag, следовательно, совершить противоположное требуемому для того, чтобы угол abg хотя бы достиг величины угла agd.

Всем этим я отнюдь не хотел предложить новый метод математических демонстраций или заменить моим доказательством доказательство Евклида; для этого оно не подходит по всему своему характеру, а также потому, что оно предполагает понятие параллельных линий, которое лишь позже встречается у Евклида; я хотел лишь показать, чтó есть основание бытия и чем оно отличается от основания познания, которое действует лишь convictio, а это нечто совсем другое, чем понимание основания бытия. То, что в геометрии стремятся действовать лишь convictio, что производит неприятное впечатление, а не пониманием основания бытия, которое, как всякое понимание, удовлетворяет и радует, послужило, вероятно, одной из причин того, что многие люди глубокого ума не склонны заниматься математикой.

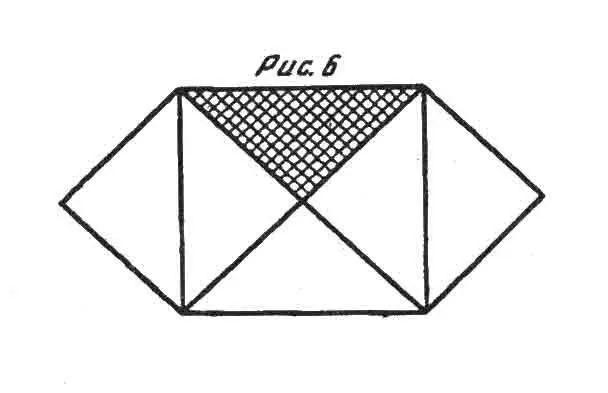
Не могу удержаться, чтобы не поместить здесь еще раз уже данную в другом месте фигуру (рис. 6); один взгляд на нее, без всяких рассуждений, убеждает в истинности теоремы Пифагора в двадцать раз больше, чем запутанное доказательство Евклида. Читатель, которого заинтересовала эта глава, найдет дальнейшее рассмотрение этой темы в «Мире как воле и представлении», т. 1, § 15 и т. 2, гл. 13.

Последний, предстоящий еще нашему рассмотрению, класс предметов способности представления очень своеобразен, но и очень важен: в нем для каждого заключен только один объект, а именно непосредственный объект внутреннего чувства, субъект воления, который есть объект для познающего субъекта и дан только внутреннему чувству; поэтому он является только во времени, не в пространстве, и даже в нем, как мы увидим, со значительным ограничением.