Авенир Уемов - Логические ошибки. Как они мешают правильно мыслить

Неприятность, вызванная логической ошибкой, в данном случае невелика. Больший вред могут причинить ошибки, допущенные в других рассуждениях.

Группа студентов физико-математического факультета педагогического института доказывала, что материя превращается в энергию, на том основании, что так написано в «Кратком философском словаре». В этом словаре действительно написаны такие слова, но его авторы не сделали никакой ошибки, хотя сама по себе мысль о превращении материи в энергию не только неистинна, но совершенно абсурдна с научной точки зрения. Логическую ошибку допустили сами студенты в рассуждении «все положения авторов философского словаря правильны, эта мысль взята из философского словаря — значит, она правильна». Логическая ошибка привела к неверному выводу.

Немалый вред могут принести и ошибочные рассуждения такого, например, типа: «он покраснел — значит, он виноват» или «если у человека повышенная температура, то он болен; у Петрова температура нормальная, следовательно, Петров здоров». В результате таких рассуждений совершенно невинного человека заподозрят и даже обвинят в каком-нибудь весьма неблаговидном поступке, а больного человека, для которого обязателен постельный режим, врач может послать на работу, что может вызвать обострение болезни.

Наконец, могут быть такие случаи, когда незамеченные логические ошибки ведут к тяжким преступлениям не только против отдельных людей, но и целых народов. Совершают ли люди эти преступления потому, что сами впадают в ошибку и делают неправильные выводы, или они сознательно вводят в заблуждение других, пользуясь их неумением отличить логически правильное рассуждение от неправильного, — в том и другом случае зло будет связано с допущением логических ошибок в обосновании истинности тех или других положений и неумением людей обнаруживать эти ошибки.

Почему люди делают логические ошибки? В чем причина того, что в одних случаях, например, в рассуждении «2 + 2 = 4, Земля вращается вокруг Солнца, следовательно, Волга впадает в Каспийское море», логическая ошибка ясна каждому здравомыслящему человеку, а в примерах с теоремой Пифагора, планом сочинения и вопросом об изучении географии многие люди логическую ошибку совсем не замечают?

Здесь одной из важнейших причин является то, что многие неправильные мысли похожи на правильные. И чем больше это сходство, тем труднее заметить ошибку. Если приведенные в начале неправильные рассуждения сопоставить с правильными, то разница может показаться не очень значительной. Многие, возможно, не заметят этой разницы даже сейчас, когда их внимание специально обращается на различие связей между мыслями в данном случае и в примерах, приведенных вначале.

I. То, что треугольник со сторонами 3, 4 и 5 прямоугольный, можно вывести из теоремы, обратной теореме Пифагора. Согласно этой теореме, если квадрат одной стороны треугольника равен квадрату двух других сторон, то этот треугольник прямоугольный. Здесь же как раз налицо такое соотношение: 5 2= З 2+ 4 2. Следовательно, данный треугольник прямоугольный.

II. План сочинения «Роман „Война и мир“ Толстого — героическая эпопея борьбы русского народа».

Главная часть:

1. Действия регулярной русской армии.

2. Поддержка русской армии народом:

а) в тылу русской армии;

б) в тылу захватчиков (партизанское движение).

III. Зачем необходимо изучать географию? Изучение географии помогает лучше понять историю развития человечества и события, происходящие в настоящий момент у нас в стране и во всем мире.

Связь мыслей в данном случае принципиально отличается от той связи, которая была установлена на приемных экзаменах в вузе и ученицей 10-го класса. Однако это различие очевидно не для всех.

Существуют рассуждения, в которых сознательно допущена логическая ошибка и отношения между мыслями при этом устанавливаются так, чтобы эту ошибку трудно было заметить. С помощью таких рассуждений обосновывается истинность заведомо ложных утверждений. При этом неправильному рассуждению так тонко придается видимость правильного, что различие между правильным и неправильным становится незаметным. Такие рассуждения называются софизмами . В древней Греции были философы-софисты, которые специально занимались составлением софизмов и обучали этому своих учеников. Одним из наиболее известных софистических рассуждений того времени является софизм Эватла. Эватл был учеником софиста Протагора, который согласился обучать его софистике с тем условием, что после первого выигранного Эватлом судебного процесса он заплатит Протагору определенную сумму денег за свое обучение. Когда обучение было закончено, Эватл заявил Протагору, что денег он ему платить не будет. Если Протагор захочет решить дело судом и процесс будет выигран Эватлом, тогда он не будет платить денег, согласно приговору суда. Если же суд решит дело в пользу Протагора, то и тогда Эватл не будет ему платить, так как в этом случае Эватл проигрывает, а по условию он должен заплатить Протагору лишь после того, как выиграет процесс. В ответ на это Протагор возразил, что, наоборот, и в том и в другом случае Эватл должен ему заплатить: если процесс выигрывает Протагор, тогда Эватл, естественно, платит ему согласно решению суда; если же выигрывает Эватл, то он опять должен платить, поскольку это будет первый выигранный им судебный процесс. То и другое рассуждение похоже на правильное, и заметить ошибку в них трудно, хотя совершенно ясно, что быть правильными одновременно оба они не могут и по крайней мере в одном из них допущена ошибка.

Много примеров того, как совершенно неправильное рассуждение облекается в форму, по всей видимости строго правильную, можно взять из области математики. К таким рассуждениям относится, например, следующее.

Квадрат со стороной 21 имеет ту же площадь, что прямоугольник со сторонами 34 (= 21 + 13) и 13.

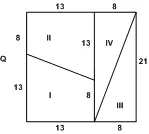
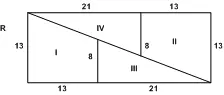
Квадрат Q (рис. 1) разделен на два прямоугольника размерами 13×21 и 8×21. Первый прямоугольник разрезан на две одинаковые прямоугольные трапеции с основаниями 13 и 8, второй прямоугольник — на два одинаковых прямоугольных треугольника с катетами 8 и 21. Из полученных четырех частей складываем прямоугольник R , как показано на рис. 2.

Точнее говоря, к прямоугольной трапеции I прикладываем прямоугольный треугольник III так, чтобы прямые углы при общей стороне 8 оказались смежными, — образуется прямоугольный треугольник с катетами 13 и 34 (= 13 + 21): точно такой же треугольник складывается из частей II и IV; наконец, из полученных двух равных прямоугольных треугольников складывается прямоугольник R со сторонами 13 и 34. Площадь этого прямоугольника равна 34×13 = 442 ( см 2), между тем как площадь квадрата Q , состоящего из тех же частей, есть 21×21=441 ( см 2). Откуда же взялся лишний квадратный сантиметр? [2] См. Я. С. Дубнов , Ошибки в геометрических доказательствах, Гостехиздат, 1953, стр. 10.