Авенир Уемов - Логические ошибки. Как они мешают правильно мыслить

Возьмем такое рассуждение:

«Бородин мог стать либо писателем, либо ученым, либо композитором. Он стал композитором. Следовательно, Бородин не был ни писателем, ни ученым».

Опыт показывает, что многие из тех, которые делают такой неправильный вывод, могут вместе с тем без особого труда справиться с задачей правильного — графического изображения отношений по объему понятий «писатели», «композиторы» и «ученые» (рис. 17).

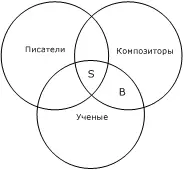
А получив такую схему, уже совсем легко понять, что Бородин (B) в принципе мог быть одновременно и тем, и другим, и третьим (S). Кстати, он был ученым-химиком. В тех случаях, когда члены деления исключают друг друга, избежать ошибки значительно легче. Если этот человек может быть или пионером, или комсомольцем и известно, что он пионер, то ясно, что он не комсомолец (рис. 18).

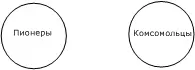
В некоторых случаях можно определить правильность или неправильность рассуждения с помощью такого приема. Если плохо усвоены или забыты правила, которые должны соблюдаться в данной форме мысли, можно эту мысль свести к другой форме, правила которой известны лучше. Например, правила условно-категорического силлогизма усвоить и применять значительно легче, чем правила категорического силлогизма. Они очень просты и кратки: необходимый вывод получается от утверждения основания к утверждению следствия и от отрицания следствия к отрицанию основания. В остальных случаях — вывод лишь вероятный.

Предположим, нам нужно проверить правильность рассуждения

«планеты вращаются вокруг Солнца;

Земля вращается вокруг Солнца;

—————————————————

Земля — планета».

Это умозаключение — категорический силлогизм. Если мы забыли правила распределенности терминов в категорическом силлогизме, то мы можем свести его к условно-категорическому: «Если Земля — планета, то она вращается вокруг Солнца. Земля вращается вокруг Солнца. Следовательно, Земля — планета». Мы видим, что вывод делается от утверждения следствия к утверждению основания. Следовательно, умозаключение неправильное.

Другой пример:

все рыбы дышат жабрами;

кит не рыба;

————————————

кит не дышит жабрами.

После замены большей посылки получаем условно-категорический силлогизм: «Если кит — рыба, то он дышит жабрами. Кит — не рыба. Следовательно, кит не дышит жабрами». Вывод делается от отрицания основания к отрицанию следствия, следовательно, он является неправильным.

Возьмем силлогизм:

все честные люди против войны;

этот человек не против войны;

————————————————

этот человек не честен.

Преобразуем этот силлогизм в условно-категорический:

если человек честен, он против войны;

этот человек не против войны;

————————————————

он не честен.

Здесь вывод сделан от отрицания следствия к отрицанию основания. Следовательно, этот вывод с необходимостью вытекает из посылок и рассуждение является правильным.

Наконец, можно обнаружить, что в рассуждении есть какая-то ошибка, путем подбора определенного факта из жизни, несовместимого с данным выводом. Если этот вывод сделан из истинных посылок, то наличие такого факта явно будет указывать на наличие ошибки в рассуждении, например:

в правильно решенной задаче результат совпадает с ответом, данным в задачнике;

в этой задаче результат совпадает с ответом, данным в задачнике;

———————————————————————————————————

следовательно, эта задача решена правильно.

Если человек может привести хотя бы один такой факт или даже просто быть уверенным в возможности такого факта, когда в задаче, решенной неправильно, ответ совпадает с заданным, то тем самым он докажет, что вывод в данном случае сделан неправильно.

Разумеется, все эти приемы не могут заменить логических навыков, основанных на знании правил логики. Каждый из них по-своему ограничен и не может дать полной гарантии от ошибок в рассуждениях. Метод аналогии связан с необходимостью придумывать в каждом отдельном случае какой-то пример для сравнения, что удается далеко не всем и не всегда. К тому же применение аналогии без знания ее правил может привести к ошибочной аналогии. В результате сама проверка правильности рассуждения окажется неправильной. Применяя аналогию, нужно строго следить за тем, чтобы логическая форма того рассуждения, которое берется для сравнения, в точности совпадала с формой того рассуждения, правильность которого проверяется. В этом случае будет выполняться и первое правило аналогии о совпадении признаков или отношений в сравниваемых предметах и второе правило — о том, что если интересующий признак есть в одном предмете, то он есть и в другом. В самом деле, нас интересует в данном случае правильность вывода. А вывод в умозаключениях определяется, как мы знаем, исключительно строением умозаключения, его логической формой. Значит, если в умозаключении определенного строения вывод правильный, он обязательно будет правильным и в другом умозаключении, имеющем точно такое же строение. Другими словами, признак, сосуществующий с остальными признаками в одном предмете, сосуществует и в другом. Конечно, во многих случаях интуитивно удается подбирать правильные аналогии. Но это далеко не всегда. А ошибка в аналогии может привести к неправильному признанию или отрицанию того вывода, который проверяется с помощью этой аналогии.

Так, вывод «квадрат является равносторонним четырехугольником, следовательно, всякий равносторонний четырехугольник есть квадрат» является, несомненно, правильным. По аналогии с ним строится рассуждение «квадрат является фигурой с взаимно-перпендикулярными диагоналями, следовательно, всякая фигура с взаимно-перпендикулярными диагоналями есть квадрат». Однако ромб имеет взаимно-перпендикулярные диагонали, но ромб — это не квадрат. Следовательно, аналогия является неправильной. Почему? Потому что для сравнения взяты рассуждения, логически различные: в первом случае имеется общеутвердительное суждение, являющееся определением, поэтому его можно обращать в общеутвердительное; во втором случае — общеутвердительное суждение, не являющееся определением, поэтому его можно обращать только в частно-утвердительное: «некоторые фигуры с взаимно-перпендикулярными диагоналями — квадраты».