Карл Поппер - Объективное знание. Эволюционный подход

Рисунок Ньютона иллюстрирует его высказывание, что если скорость снаряда, а вместе с ней и дальность полета, возрастает, он «в конце концов, выйдя за пределы Земли... уйдет в пространство, не касаясь ее» [193].

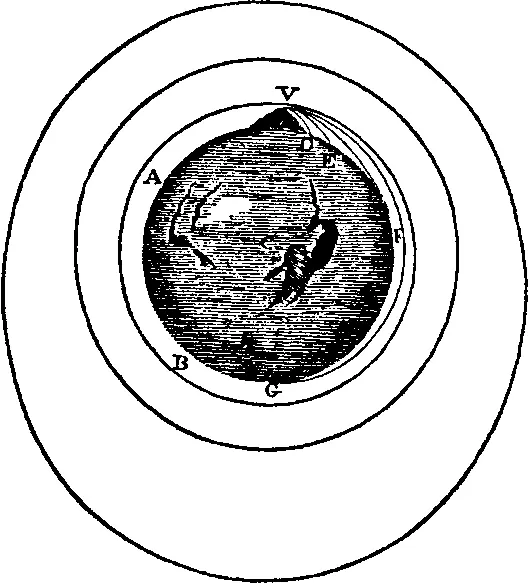
Итак, пущенный на Земле снаряд движется не по параболе, а по эллипсу. Конечно, для достаточно коротких расстояний парабола дает очень хорошее приближение, но параболическую траекторию нельзя считать в строгом смысле выводимой из теории Ньютона, если только мы не добавим к ней фактически ложное начальное условие (которое, кстати, не реализуемо в теории Ньютона, поскольку приводит к абсурдным следствиям), а именно — что радиус Земли бесконечно велик. Если мы не принимаем этого допущения, даже хотя известно, что оно ложно, то мы всегда получим эллипс — в противоречие с законом Галилея, согласно которому мы должны получить параболу.

В точности аналогичная ситуация возникает в связи со второй частью закона Галилея, утверждающего существование постоянного ускорения. С точки зрения теории Ньютона ускорение свободно падающего тела никогда не бывает постоянным — оно все время возрастает по мере падения в силу того, что тело приближается к центру притяжения. Этот эффект очень значителен, если тело падает с большой высоты, хотя, конечно, он будет пренебрежимо мал, если высота падения пренебрежимо мала по сравнению с радиусом Земли. В этом случае мы можем получить теорию Галилея из теории Ньютона, если снова введем ложное предположение, что радиус Земли бесконечен (или высота падения равна нулю).

Противоречия, на которые я указал, далеко не пренебрежимо малы для ракет, рассчитанных для полета на дальние дистанции. К ним мы можем применять теорию Ньютона (конечно, с поправками на сопротивление воздуха), но не теорию Галилея: последняя даст просто ложные результаты, как легко показать с помощью теории Ньютона.

С законами Кеплера ситуация аналогична. Очевидно, в рамках теории Ньютона законы Кеплера верны лишь приближенно, то есть в строгом смысле неверны, и это особенно ясно, если принять во внимание взаимное притяжение планет [194]. Но помимо этого довольно очевидного противоречия, между теориями Ньютона и Кеплера есть и более фундаментальные противоречия. Ведь даже если — в виде уступки нашим оппонентам — мы пренебрежем взаимным притяжением планет, то третий закон Кеплера, рассматриваемый с точки зрения ньютоновской динамики, не может быть чем-то большим, нежели просто приближением, применимым только в очень особом случае — к планетам, массы которых равны, а если не равны, то пренебрежимо малы по сравнению с массой Солнца. А поскольку это условие даже приближенно не выполняется в случае, когда одна планета очень легкая, а другая очень тяжелая, то ясно, что третий закон Кеплера противоречит теории Ньютона точно так же, как закон Галилея.

Это легко показать следующим образом. В теории Ньютона можно сформулировать для системы двух тел — двоичной звездной системы — закон, который астрономы часто называют «законом Кеплера», поскольку он тесно связан с третьим законом Кеплера. Этот так называемый «закон Кеплера» говорит, что если то есть масса одного из этих двух тел, скажем, Солнца, а т 1 — масса второго тела, скажем, планеты, то выбрав подходящие единицы измерения, мы можем вывести из теории Ньютона следующее равенство:

(1): a 3/T 2=m 0+m 1,

где а — среднее расстояние между этими двумя телами, а T — время полного обращения [планеты вокруг Солнца]. Третий же закон Кеплера утверждает, что

(2): a 3/T 2= const

то есть а 3/Т 2 постоянно для всех планет Солнечной системы. Ясно, что мы можем получить этот закон из (1) только при допущении, что т 0+ m 1= const; а поскольку для нашей солнечной системы m 0постоянна, мы получим (2) из (1), если примем, что m 1 одна и та же для всех планет; или, если это фактически ложно (как это и есть на самом деле, поскольку Юпитер в несколько тысяч раз больше, чем самые маленькие планеты), — что массы планет все равны нулю по сравнению с массой Солнца, так что мы можем положить т 1 = 0 для всех планет. Это очень хорошее приближение с точки зрения теории Ньютона; но в то же время равенство т 1 = 0 не только, строго говоря, ложно, но и нереализуемо с точки зрения теории Ньютона. (Тело с нулевой массой не подчинялось бы ньютоновским законам движения). Так что даже если мы забудем о взаимном притяжении планет, третий закон Кеплера (2) противоречит теории Ньютона, из которой выводится (1).

Важно отметить, что из теорий Галилея или Кеплера мы не получаем даже малейшего намека на то, как следовало бы приспосабливать эти теории — какие ложные допущения надо было бы принимать или какие условия оговаривать, — если бы мы захотели перейти от этих теорий к другой, более общей, такой как теория Ньютона. Только после того, как мы получим теорию Ньютона, мы сможем выяснить, можно ли и в каком смысле назвать эти более старые теории приближениями к ней. Мы можем кратко выразить этот факт, сказав, что хотя с точки зрения теории Ньютона теории Кеплера и Галилея являются прекрасными приближениями к некоторым особым ньютонианским результатам, однако нельзя сказать, что с точки зрения двух других теорий теория Ньютона является приближением к их результатам. Все это показывает, что логика — ни дедуктивная, ни индуктивная — не может сделать шаг от этих теорий к динамике Ньютона [195]. Этот шаг может сделать только изобретательность. А после того, как он будет сделан, можно будет сказать, что результаты Кеплера и Галилея подкрепляют (corroborate) новую теорию.

Здесь, однако, меня интересует не столько невозможность индукции, сколько проблема глубины. А из нашего примера мы действительно можем узнать кое-что насчет этой проблемы. Теория Ньютона объединяет теории Галилея и Кеплера, однако она отнюдь не является просто конъюнкцией этих двух теорий, которые для теории Ньютона играют роль объясняемого, — объясняя их, она их корректирует. Исходной задачей объяснения был дедуктивный вывод прежних результатов. Но эта задача была решена не выводом прежних результатов, а выводом вместо них чего-то лучшего — новых результатов, которые в особых условиях старых результатов численно очень близко подходят к старым, в то же время корректируя их. Таким образом, можно сказать, что эмпирические успехи старой теории подкрепляют новую теорию; вдобавок эти корректировки в свою очередь могут быть проверены и, возможно, опровергнуты — или подкреплены. Что наиболее ярко выявляется этой логической ситуацией, так это тот факт, что новая теория никак не может быть ни ad hoc, ни круговой. Она не только не повторяет свое объясняемое, но и противоречит ему и корректирует его. При этом даже свидетельства самого объясняемого становятся независимыми свидетельствами в пользу новой теории. (Кстати, этот анализ позволяет нам объяснить ценность метрических теорий и измерения; и таким образом он помогает нам избежать ошибочного принятия измерения и точности за окончательные, ни к чему не сводимые ценности).