Джордж Эллис - Далекое будущее Вселенной Эсхатология в космической перспективе

d T= R Bsinhη. (91)

Если А передает F фотонов в стерадиан в направлении В, число фотонов, принятых В, будет составлять

F' = (F∑' / d 2 T), (92)

где ∑' — эффективное сечение приемника.

Теперь сечение приемника, поглощающего фотон с частотой ω', задано формулой, подобной формуле (63) из предыдущей лекции:

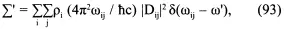
где D ij— снова дипольный матричный элемент между состояниями i и j. Проинтегрировав все это относительно всех ω', мы получаем в точности левую половину правила суммы (67). Вклад от отрицательного ω' представляет собой наведенное излучение фотонов получателем. Я предполагаю, что получатель не связан с поступающими фотонами, и, следовательно, наведенным излучением можно пренебречь. Таким образом, у нас получается

∫ 0 ∞∑'dω' = Ν' (2π 2е 2/mc), (94)

где Ν' — число электронов приемника. Если приемник настроен на частоту ω' с ширингой полосы В', (94) дает нам

Σ'Β' ≤ Ν' S 0, (95)

S 0= (2π 2e 2/mc) = 0,167 cm 2sec -1. (96)

Чтобы избежать смешивания единиц, я измеряю как ω', так и В' не в герцах, а в радианах в секунду. Полагаю, высокоразвитая цивилизация сможет создать приемник, для которого соотношение (95) выполняется со знаком равенства. Тогда (92) примет следующий вид:

F' = (FN' S 0/d 2 TB'). (97)

Я предполагаю, что передатчик содержит N электронов, способных создать направленное излучение с углом распространения, составляющим порядка N -1/2. Если передатчик представляет собой луч, состоящий из N диполей с оптимальными фазами, число фотонов на стерадиан в луче составляет

F = (3N/8π) (E/hω), (98)

где Е — общий объем переданной энергии. Число полученных фотонов равняется

F' — (3NN 1ES 0/ 8πhωd 2 TB'). (99)

Из (99) мы сразу видим, что для увеличения числа передаваемых фотонов необходимы низкие частоты и узкие полосы. Однако мы заинтересованы в передаче не фотонов, а информации. Чтобы эффективно извлекать информацию из заданного числа фотонов, нам придется использовать ширину полосы, равную скорости детектирования:

B' = (F'/τ B), B = (F'/τ A), (100)

где τ в— продолжительность приема, а τ А— продолжительность передачи. При этой ширине полосы F' представляет как число фотонов, так и число принятых битов информации. Удобно выражать τ ви τ Акак долю радиуса вселенной во время передачи и приема информации:

τ A= (δR A/c), τ B= (δR B/c). (101)

Условие

δ ≤ 1 (102)

устанавливает нижний предел ширины полосы В. Предположим также для простоты, что частота со сделана такой низкой, как только возможно, в соответствии с шириной полосы В, а именно:

ω = В, ω' = В'. (103)

Тогда (99), (100) и (101) дают

F' = {NN'5 2E / [(1+z) (sinh 2η)E c]} 1/3, (104)

где, согласно (96),

Е с= (8πhc 2/ 3S 0) = (4/3π)137mc 2= 3∙10 5erg. (105)

Из (104) мы видим, что количество информации, которую можно передать от А к В через заданный объем энергии, со временем, по мере расширения вселенной и отдаления А и В друг от друга, не уменьшается. Увеличение расстояния компенсируется снижением энергетической стоимости каждого фотона и увеличением угла приема при уменьшении длины волны.

Полученный сигнал задается формулой (104). Теперь нам необходимо сравнить его с полученным шумом. Фоновый шум во вселенной на частоте со можно описать эквивалентной температурой шума T N, так что число фотонов на единицу волны на стерадиан на квадратный сантиметр в секунду описывается формулой Релея–Джинса:

I(ω) = (kT Nω / 4π 3hc 2). (106)

Эта формула — просто определение TN, которое в целом представляет собой функцию со и t. Я не предполагаю, что шум обладает планковским спектром на всех частотах. Лишь часть шума принадлежит изначальной фоновой радиации, обладающей планковским спектром при температуре θ R. Изначальная шумовая температура θ Rизменяется обратно пропорционально радиусу вселенной:

(kθ RR/hc) = Λ= 10 29, (107)

где R задано формулой (8). Я полагаю, что спектр шума в целом по мере расширения вселенной изменяется в том же соотношении с радиусом и таким образом:

(T N/θ R) = f(x), х = (hω/kθ R), (108)

где f есть универсальная функция от х. Если х близко к единице, то в шуме преобладает реликтовое излучение и f(x) имеет планковскую форму

f(x) = f P(x) = х (е х— 1) -1, х ~ 1. (109)

Однако возможны значительные отклонения от (109) как при большом х (результате красного смещения звездного света), так и при маленьком х (результате нетермальных радиоизлучений). Не углубляясь в детали, скажем просто, что f(x) в целом является уменьшающейся функцией х и быстро стремится к нулю по мере того, как х —> ∞.

Общая энергетическая плотность радиации во вселенной составляет

(4π/c) ∫I(ω) hωdω = (kθ R) 4I / (π 2h 3c 3), (110)

где

I = ∫ 0 ∞f(x)x 2dx. (1ll)

Интеграл I должен сходиться как при высоких, так и при низких частотах. Следовательно, мы можем найти такое числовое ограничение b, что

x 3f(x)

для всех х. В сущности, (112), вероятно, выполняется при b = 10, если мы будем избегать некоторых определенных частот, например водородной линии 1420 Мгц.

Число шумовых фотонов, полученных в течение времени tB приемником с шириной полосы В' и сечением составляет

F N= 4π∫'B'τ BI(ω'). (113)

Подставляя значения из (95), (96), (100), (103) и (108) в (113), получаем:

F N= (2r 0/λ B)fN'F', (114)

где

r 0= (e 2/mc 2) = 3∙10–1 3cm, (115)

а

λ B= (hc / kθ' R) = Λ -1R B(116)

— длина волны фонового реликтового излучения во время приема сообщения. Если F' — сигнал, то отношение сигнала к шуму равняется

R SN= (λ B/ 2fN'r 0). (117)

В этой формуле f — отношение шума и температуры, заданное (108), N' — число электронов приемника, а ρ 0, λ Bзаданы (115) и (116). Отметим, что в вычислении (117) мы не даем приемнику возможности выбора угла, поскольку сечение заданное (95), не зависит от направления.

Теперь подведем итоги нашего анализа. У нас имеются передатчик и приемник на мировых линиях А и В, передающие и принимающие сигналы во время t A= Т 0(sinhξ — ξ), t B= Т 0(sinh(ξ + η) — (ξ + η)). (118)

Согласно (89) и (101),

τ A= δ(dt A/dξ), τ B= δ(dt B/dξ). (119)

Для удобства будем считать, что передатчик постоянно направлен на приемник и передает сообщения с определенным циклом 8, который может изменяться в зависимости от Когда 5 = 1, передатчик все время включен. Число F' фотонов, принимаемых во время τ в, может рассматриваться как количество битов в отношении к переменной ξ. В сущности, F'dξ — это число битов, получаемых в интервале dξ. Работать с переменной ξ полезно, поскольку она поддерживает постоянное различие л между А и В.

Из (100), (101), (103), (107) и (108) мы выводим простую формулу количества битов:

F = Λхδ. (120)

Энергия Е, переданная во время τ А, может также рассматриваться как скорость передачи энергии в единицу интервала Из (104) и (120) мы выводим

Е = (Λ 3/ NN') (1 + z) (sinh 2η)x 3δE c. (121)

Мы все еще можем свободно выбирать параметры х [определяя частоту со согласно (108)] и 5, оба из которых могут изменяться в зависимости от Единственные ограничения — (102) и сигнально–шумовое условие