Рене Декарт - Сочинения в двух томах. Том 1

Если нужно произвести сложение или вычитание, мы представляем себе предмет в виде линии или в виде протяженной величины, в которой должна быть рассмотрена только длина: действительно, если нужно прибавить линию

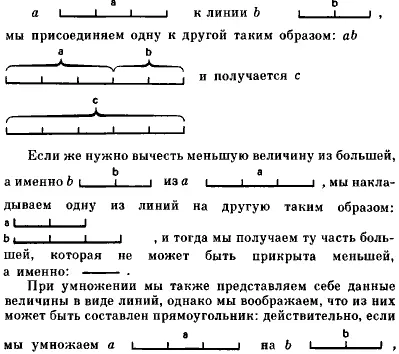
мы прикладываем одну линию к другой под прямым углом таким образом:

и получается прямоугольник

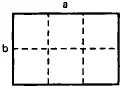
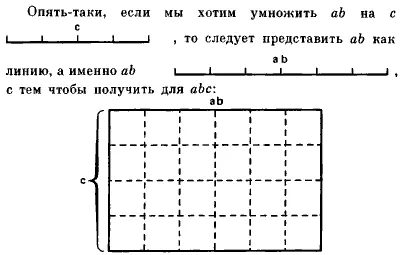
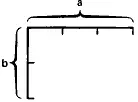
Наконец, при делении, в котором дан делитель, мы воображаем, что делимая величина представляет собой прямоугольник, одна сторона которого является делителем, а другая — частным; так, если прямоугольник ab нужно разделить на а,

из него убирают ширину а, и остается b в качестве частного: 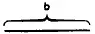. Или, наоборот, если тот же прямоугольник делят на b, то убирают высоту b, и а будет частным: .

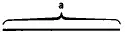Что же касается тех делений, в которых делитель не дан, а только обозначен через посредство какого-либо отношения, как, например, когда говорится, что нужно извлечь квадратный или кубический корень и т. д., то следует отметить, что в этих случаях и подлежащий делению, и все другие термины нужно всегда представлять себе как линии, расположенные в ряде непрерывно пропорциональных величин, первой из которых является единица, а последней — делимая величина. О том, каким образом между этой величиной и единицей должно быть найдено сколько угодно средних пропорциональных, будет сказано в своем месте. Теперь же достаточно уведомить, что здесь, как мы предполагаем, подобные действия еще не были доведены до совершенства, так как они должны производиться при посредстве непрямых и обратных актов воображения, а сейчас мы говорим только о вопросах, которые следует обозревать прямо.

Что касается других действий, то они, конечно, весьма легко могут быть осуществлены тем способом, которым, как мы сказали, их надлежит понимать. Вместе с тем остается изложить, каким образом должны быть подготовлены используемые в них термины; ибо, хотя, впервые занимаясь каким-либо затруднением, мы вольны представлять себе его термины как линии или как прямоугольники и никогда не приписывать этим терминам других фигур, как было сказано в четырнадцатом правиле, тем не менее в рассуждении часто бывает, что прямоугольник, после того как он был образован умножением двух линий, затем следует представлять себе в виде линии, для того чтобы выполнить другое действие, либо тот же самый прямоугольник или линию, полученную в результате какого-то сложения или вычитания, затем следует представлять себе как некоторый другой прямоугольник, построенный на обозначенной линии, которой он должен быть разделен.

Итак, здесь стоит изложить, каким образом всякий прямоугольник можно преобразовать в линию и в свою очередь линию или даже прямоугольник — в другой прямоугольник, сторона которого обозначена. Это весьма легко сделать геометрам, если только они заметят, что в виде линий, всякий раз когда мы, как здесь, сравниваем их с каким-либо прямоугольником, мы неизменно представляем себе прямоугольники, одна сторона которых является той длиной, какую мы приняли за единицу. Ведь тогда вся эта задача сводится к положению такого вида: по данному прямоугольнику построить другой, равный ему, на данной стороне.

Хотя это действие известно даже новичкам в геометрии, тем не менее мне хочется объяснить его, чтобы не показалось, будто я что-либо упустил.

Посредством этого метода рассуждения нужно отыскивать столько величин, выраженных двумя различными способами, сколько неизвестных терминов мы допускаем в качестве известных, для того чтобы прямо обозреть затруднение; ибо таким образом мы будем иметь столько же сравнений между двумя равными терминами.

Отыскав уравнения, нужно произвести опущенные нами действия, ни в коем случае не пользуясь умножением тогда, когда будет уместно деление.

Если имеется много таких уравнений, их все необходимо свести к одному, а именно к тому, члены которого займут меньшее число ступеней в ряде непрерывно пропорциональных величин, соответственно каковому они и должны быть расположены по порядку.

Конец

Разыскание истины посредством естественного света, который сам по себе, не прибегая к содействию религии или философии, определяет мнения, кои должен иметь добропорядочный человек относительно всех предметов, могущих занимать его мысли, и проникает в тайны самых любопытных наук

Добропорядочный человек не обязан перелистать все книги или тщательно усвоить все то, что преподают в школах; более того, если бы он потратил чересчур много времени на изучение книг, это образовало бы некий пробел в его воспитании. В течение жизни ему необходимо совершить много иных дел, и его жизненный досуг должен быть распределен настолько верно, чтобы большая часть этого досуга отводилась на свершение добрых дел, понятие о которых бывает ему внушено его разумом, даже если он иных наставлений не получает. Однако в этот мир он приходит невежественным, и, поскольку ранние его познания основываются лишь на неразвитом чувственном восприятии и на авторитете его наставников, почти невозможно, чтобы воображение его не оказалось в плену бесчисленных ложных мыслей до того, как его разум примет на себя руководящую роль, и в дальнейшем ему нужны большая сила характера или же наставления какого-либо мудреца — как затем, чтобы избавиться от занимающих его ум ложных теорий, так и для того, чтобы заложить первоосновы прочного знания и открыть себе все пути, идя которыми он может поднять свои знания на высшую доступную ему ступень.

Об этих-то вещах я и решил написать в данном труде, дабы пролить свет на истинные богатства наших душ и указать каждому человеку средства для отыскания в самом себе, без заимствований у других, всего того знания, какое необходимо ему для правильного жизненного поведения и для последующего достижения — с помощью самостоятельных занятий — всех тех самых интересных знаний, какими может располагать человеческий разум.