Рене Декарт - Сочинения в двух томах. Том 1

Причина, препятствующая им продвинуться к этому пространству, заключается в том, что все движения продолжаются по возможности по прямым линиям и, следовательно, когда природа имеет много путей для достижения одного и того же результата, она всегда безошибочно выбирает самый короткий. Ибо если бы частицы второго элемента, находящиеся, например, у К, продвинулись к Е, то все те частицы, которые были ближе к Солнцу, в тот же самый миг продвинулись бы к тому месту, которое покинули первые. Таким образом, результат движения этих частиц был бы лишь тот, что одновременно с заполнением пространства Е образовалось бы другое пустое пространство равной величины на поверхности ABCD. Но совершенно ясно, что тот же самый результат тем более получился бы, если бы частицы, находящиеся между линиями AF и DG, продвинулись совершенно прямо к Е. Следовательно, если нет ничего препятствующего этим частицам продвинуться к Е, остальные частицы туда совершенно не стремятся, подобно тому как камень никогда не падает к центру Земли по кривой, если он может сделать это по прямой.

Наконец, обратите внимание на то, что все частицы второго элемента, находящиеся между линиями AF и DG, должны вместе продвинуться к этому пространству Е, чтобы заполнить его в тот самый момент, когда оно окажется пустым. Их двигает туда одно только стремление удалиться от пункта S. Хотя это стремление и приводит как будто к тому, что частицы, находящиеся между линиями BF и CG, стремятся туда более прямо, чем частицы, остающиеся между линиями AF и BF, DG и CG, тем не менее эти последние не менее расположены направиться туда, чем первые. Это станет очевидным, если вы обратите внимание на результат их движения. Я сказал, что пространство Е заполняется и одновременно на поверхности ABCD делается пустым другое пространство, одинаковой с ним величины. Изменение положения частиц при переходе их из места, занимавшегося ими ранее, в новое, где они остаются после заполнения пространства Е, не имеет значения, поскольку частицы следует предположить столь равными и столь подобными друг другу во всем, что не имеет значения, какими из них заполнено каждое из этих мест. Тем не менее отсюда нельзя сделать вывод, что все частицы равны; можно только сказать, что движения, причиной которых может быть неравенство частиц, не относятся к действию, о котором мы говорим.

Нет более простого способа наполнить часть пространства Е, например ту, которая одновременно освобождается у D, как направить к Е все частицы материи, находящиеся на прямой линии DG или DE. Если бы первыми продвинулись к этому пространству Е только частицы, находящиеся между линиями BF и CG, то они оставили бы пустое пространство около V, которое должны были бы занять частицы, находящиеся у D. Таким образом, действие, произведенное движением материи, находящейся на прямой линии DG или DE, было бы произведено и движением материи, находящейся на кривой линии DVE, что противоречило бы законам природы.

Но если вам не совсем понятно, каким образом частицы второго элемента, находящиеся между линиями AF и DG, могут все вместе продвинуться к Е, когда расстояние между А и D больше, чем между F и G, и пространство, куда они должны войти, чтобы продвинуться к Е, теснее, чем то, откуда они должны выйти, то нужно принять во внимание, что действие, посредством которого они стремятся удалиться от центра своего неба, заставляет их касаться не тех из соседних с ними частиц, которые находятся на одинаковом с ними расстоянии от этого центра, а тех, которые несколько больше удалены от него. Например (рис. 7), тяжесть маленьких шариков 1, 2, 3, 4, 5 заставляет соприкасаться друг с другом не те из них, которые обозначены одной и той же цифрой, а те, которые обозначены разными цифрами; она заставляет шарики, обозначенные цифрой 1 или 10, опираться на шарики, обозначенные цифрой 2 или 20, эти последние — на шарики, обозначенные 3 или 30, и т. д. Таким образом, эти шарики могут быть расположены не только так, как это изображено на рис. 7, но и так, как это изображено на рис. 8 или 9, и тысячью других различных способов.

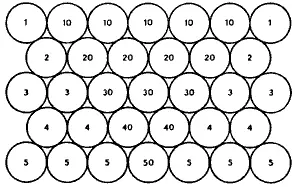
Рис. 7

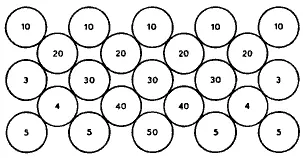
Рис. 8

Затем необходимо принять во внимание, что частицы второго элемента, двигаясь независимо друг от друга, никогда не могут находиться в таком порядке, как это изображено на рис. 7, и что только в этом единственном случае может иметь место указанное выше затруднение. Нельзя предполагать, что между частицами второго элемента, находящимися на одинаковом расстоянии от центра своего неба, имеется столь небольшой промежуток, что он был бы недостаточным для того, чтобы объяснить, почему стремление частиц удалиться от этого центра должно заставлять те из них, которые находятся между линиями AF и DG, продвигаться вместе к пространству Е, когда оно пусто. Подобно этому, на рис. 9 в отличие от рис. 10 вы видите, что тяжесть маленьких шариков 40 и 30 и т. д. должна заставлять их все вместе падать в пространство, которое занимает шарик, обозначенный цифрой 50, тотчас же, как только последний сможет оттуда выйти.

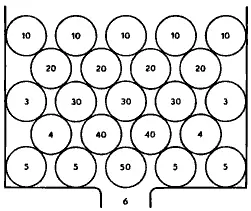
Рис. 9

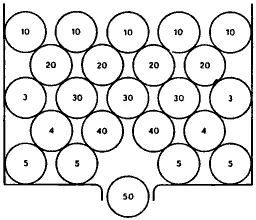
Рис. 10

Здесь совершенно ясно видно, каким образом шарики, обозначенные одной и той же цифрой, приближаясь друг к другу, располагаются в более тесном пространстве, чем то, которое они покидают. Можно также заметить, что оба шарика, обозначенные цифрой 40, должны упасть немного скорее и соответственно подойти друг к другу ближе, чем три шарика, обозначенные цифрой 30, последние — скорее и ближе, чем четыре, обозначенные цифрой 20, и т. д.

Вы, может быть, скажете, что на рис. 10 два шарика 40, 40, немного опустившись, придут в соприкосновение друг с другом и по этой причине остановятся, не имея возможности опуститься ниже. Точно так же частицы второго элемента, которые должны продвинуться к Е, вопреки нашему предположению могут остановиться, не заполнив всего пространства.

Но я отвечу на это, что частицы не могут продвинуться так мало, чтобы этого не было достаточно для доказательства того, что я сказал. Когда все имеющееся там пространство заполнено любыми телами, частицы непрерывно оказывают давление на эти тела и действуют на них как бы затем, чтобы столкнуть их с места.

Кроме того, можно указать, что другие движения частиц во время их перемещения к E ни на один момент не дают им возможности оставаться в таком порядке, как на рис. 10, мешают им соприкасаться друг с другом или даже заставляют их после соприкосновения немедленно разделиться. Таким образом, частицы непрерывно продвигаются к пространству Е до тех пор, пока оно не наполнится. Следовательно, отсюда можно сделать только тот вывод, что сила, с которой они стремятся к Е, как будто колеблется: то увеличивается, то ослабевает небольшими толчками в соответствии с изменением положения частиц. Это свойство представляется весьма похожим на свет.