Юрий Ивлев - Логика для юристов: Учебник.

Объем понятия – это множество предметов, обобщаемых и выделяемых в понятии, т.е. множество предметов, которые характеризуются системой признаков, составляющей содержание понятия.

Естественно различать логический и фактический объемы понятия.

Логический объем – это класс предметов, обладающий системой признаков, составляющей логическое содержание понятия.

Фактический объем – это класс предметов, обладающий системой признаков, составляющей фактическое содержание понятия.

Отдельные предметы, относящиеся к классу предметов, представляющему собой объем понятия, называют элементами объема понятия . Элементами объема понятия о человеке являются отдельные люди. Подклассы объема понятия, не совпадающие с ним и не являющиеся пустым множеством, называются частями объема .

Объем понятия можно представить графически в виде круга, заполненного точками. Каждая точка этого круга представляет какой-то один элемент объема понятия. Например, объем понятия о человеке графически можно представить в виде круга А .

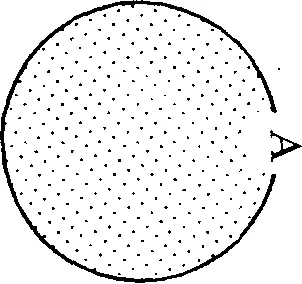
Связь между содержанием и объемом понятия выражается в логическом законе обратного отношения между ними, который можно сформулировать так: пусть имеются два понятия, содержание одного из которых меньше содержания второго, тогда объем первого больше объема второго.

Например, сравнивая содержание понятий “преступление” и “хозяйственное преступление”, мы можем утверждать, что содержание первого меньше, чем содержание второго. Объемы же этих понятий находятся в обратном отношении, поскольку хозяйственных преступлений меньше, чем всех преступлений.

В традиционной логике не было точных критериев сравнения понятий по содержаниям. Считалось, что содержание одного понятия больше содержания другого, если содержание первого включает в себя больше признаков, чем содержание другого. В тех случаях, когда признаки объединены союзом “и”, такое понимание может быть приемлемо, но не всегда. Так, содержание понятия “число, которое делится на 2 и 3” больше содержания понятия “число, которое делится на 2”. Если же сравнить понятия “число, которое делится на 2 и 3” и “число, которое делится на 2”, то окажется, что сравнение содержаний по количеству признаков не позволяет установить, какое понятие больше по содержанию.

В традиционной логике не различались логические и фактические содержания, а также логический и фактический объемы. Все это ставило под сомнение правильность закона обратного соотношения. Приводились случаи отношений между объемами и содержаниями понятий, противоречащие закону. Известен следующий пример Больцано: содержание понятия (1) “человек, знающий все живые европейские языки”, по его мнению, больше содержания понятия (2) “человек, знающий все европейские языки”, но и объем первого понятия больше объема второго.

Содержание понятия (1) больше содержания понятия (2), если и только если из первого содержания следует второе, а обратное неверно, то есть если и только если информация, выражаемая содержанием второго, является частью информации, выражаемой содержанием первого понятия, и обратное неверно.

Какое из содержаний “знает все живые европейские языки” и “знает все европейские языки” информативнее? Из того, что человек знает все европейские языки, следует что он знает все живые европейские языки, обратное же не имеет места. Следовательно, содержание понятия (2) примера Больцано больше содержания понятия (1). Объемы же этих понятий находятся в обратном отношении. Таким образом, проблема, сформулированная Больцано, легко разрешима.

Пример, подтверждающий необходимость различать фактическое и логическое содержания, а также фактический и логический объемы. Пусть даны понятия (1) “живое существо, обладающее членораздельной речью”; (2) “живое существо, обладающее абстрактным мышлением и членораздельной речью”. Логическое содержание второго из них больше логического содержания первого, так как из наличия у предметов двух признаков следует наличие одного из них. Очевидно, что объемы этих понятий одинаковы. Как быть? Нужно различать указанные выше объемы содержаний и объемов. Здесь сопоставлялись логические содержания понятий (1) и (2), и их фактические объемы. Очевидно, что, используя наши знания о соотношении признаков человека, т.е. сопоставляя фактические (полные) содержания, мы обнаружим, что эти содержания равны.

Упражнение 4

Укажите фактические и логические объемы и содержания следующих понятий.

1. “Город с населением более миллиона человек”.

2. “Город России с населением более миллиона человек”.

3. “Самый большой город России”.

4. “Разумное животное”.

5. “Разумное животное, обладающее членораздельной речью”.

6. “Наука о мышлении”.

7. “Наука об обществе”.

Упражнение 5

Проанализируйте следующее рассуждение, используя полученные знания об объеме и содержании понятия.

«Больцано пытался критиковать закон обратного отношения между объемом и содержанием понятия традиционной логики, но безуспешно. В доказательство несостоятельности этого закона он приводил, в частности, следующий пример: объемы понятий “круглый шар” и “шар” одинаковы, но содержание первого больше содержания второго. Но этот пример не может поколебать закон обратного отношения между объемом и содержанием понятия. Дело в том, что шар — это геометрическое тело, получающееся при вращении круга вокруг своего диаметра, поэтому каждый шар — это круглый шар и, следовательно, содержание понятий “круглый шар” и “шар” одинаково.» (Кондаков Н.И. Логический словарь-справочник. М., 1975. С. 71)

Понятия делятся на виды по: (1) количественным характеристикам объемов понятий ; (2) типу обобщаемых предметов ; (3) характеру признаков, на основе которых обобщаются и выделяются предметы. Большей частью эта классификация относится к простым понятиям (понятиям, содержаниями которых являются простые признаки).

По количеству обобщаемых предметов понятия делятся на понятия с пустым (нулевым) объемом и понятия с непустым (ненулевым) объемом.

Пустым по объему называется понятие, в объеме которого нет ни одного предмета из универсума рассуждения. Содержаниями таких понятий являются системы признаков, не принадлежащие ни одному предмету из универсума. Примеры: (1) “вечный двигатель”; (2) “вещество, являющееся металлом и не являющееся электропроводным”; (3) “человек, знающий все европейские языки, но не знающий болгарского языка, являющегося европейским”.