Вячеслав Кириллов - Логика: учебник для юридических вузов

Широко применяется классификация в правовых науках. Примером может служить система права, которая включает отрасли: государственное право, финансовое право и т. д. Каждая отрасль права включает в себя правовые институты.

Вместе с тем всякая классификация относительна. Многие явления природы и общественной жизни не могут быть отнесены безоговорочно к какой-либо определенной группе явлений. Например, семью как общественно-историческое явление нельзя целиком отнести к какой-либо одной области социальной жизни, семья характеризуется как материальными, так и духовными процессами. Кроме того, с развитием знаний классификация, как правило, изменяется, дополняется, иногда заменяется новой, более точной. Поэтому ни к одной классификации нельзя подходить как к завершенной. Необходимо учитывать, что и сама действительность, и знания о ней находятся в непрерывном процессе изменения и развития.

1. Что такое деление понятия?

2. Как строится деление по видообразующему признаку и дихотомическое деление?

3. Каким правилам подчиняется операция деления понятия?

4. Что представляет собой классификация?

При помощи логических операций из двух или нескольких классов могут быть образованы новые классы. К этим операциям относятся: объединение классов, вычитание классов, пересечение классов и образование дополнения к классу.

В операциях с классами приняты следующие обозначения: А, В, С,... — произвольные классы, 1— универсальный класс, 0— нулевой (пустой) класс, символ ∪ обозначает объединение классов (сложение), символ ∩ — пересечение классов (умножение), А' (не-А)— дополнение к классу А(отрицание). В операциях с классами обычно используются круговые схемы, универсальный класс обозначается прямоугольником.

Операция объединения классов (сложение)состоит в объединении двух или нескольких классов в один класс, состоящий из всех элементов, входящих в слагаемые классы.

Операция объединения классов записывается с помощью символа сложения А ∪ В. Множество, полученное в результате сложения, называется суммой (на схеме полученное множество заштриховано).

Складывать можно множества, находящиеся в любых отношениях, например, множества, входящие в понятия, находящиеся в отношении подчинения: «юрист» ( В) и «следователь» ( А). Множество, полученное в результате сложения, включает юристов-следователей и юристов- неследователей (схема 14). Объединяя классы, находящиеся в отношении частичного совпадения: «юрист» (А) и «депутат Государственной Думы» ( В), — получим множество, объединяющее юристов-недепутатов (1), юристов-депутатов (2) и депутатов-неюристов (3) — схема 15.

Операция вычитания классовдает класс, состоящий из элементов, исключающих элементы вычитаемых классов. Вычитая, например, элементы класса «следователь» ( А) из класса «юрист» ( В), получаем класс юристов-неследователей (схема 16). Вычитая элементы класса «юрист» ( А) из класса «депутат Государственной Думы» ( В), получаем класс депутатов Государственной Думы, не являющихся юристами. Множество, полученное в результате вычитания классов, заштриховывается (схема 17).

Операция пересечения классов (умножение)состоит в отыскании элементов, общих для двух или нескольких классов (множеств). Так, в результате умножения множеств, мыслящихся в понятиях «юрист» ( А) и «депутат» ( В), получаем новое множество: юристов-депутатов (схема 18).

Схема 14

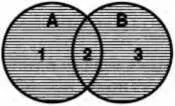
Схема 15

Схема 16

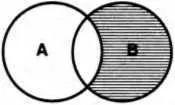
Схема 17

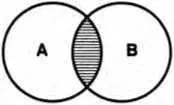
Схема 18

Операция пересечения классов записывается с помощью символа умножения: А ∩ В. Множество, полученное в результате умножения, называется произведением (заштрихованная часть схемы). Умножать можно три и больше множеств. Так, умножая множества, входящие в понятия «юрист» ( А), «депутат» ( В) и «москвич» ( С), получаем множество юристов, являющихся депутатами и москвичами (схема 19).

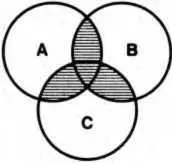
Схема 19

При умножении множеств, входящих в несовместимые понятия, например «следователь» и «адвокат», получаем нулевой (пустой) класс, так как элементов, входящих одновременно в оба понятия, не существует.

Образование дополнения (отрицание). Дополнением к классу Аназывается класс не-А (А'), который при сложении с А образует универсальную область. Эта область представляет собой универсальный класс и обозначается знаком 1. Чтобы образовать дополнение, нужно класс А исключить из универсального класса: 1 − А = А'. Образование дополнения состоит, таким образом, в образовании нового множества путем исключения данного множества из универсального класса, в который оно входит. Так, исключая множество адвокатов из универсального класса юристов, образуем дополнение: множество юристов-неадвокатов. В своей сумме оба понятия образуют весь универсальный класс, соответствующий понятию «юрист» (схема 20).

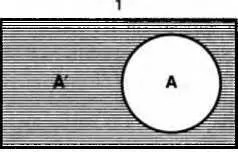
Схема 20

1. Как образуются новые классы с помощью логических операций объединения классов (сложения), вычитания классов, пересечения классов?

2. Что представляет собой образование дополнения к классу?

Познавая окружающий мир, человек раскрывает связи между предметами и их признаками, устанавливает отношения между предметами, утверждает или отрицает факт существования предмета. Эти связи и отношения отражаются в мышлении в форме суждений, представляющих собой связь понятий. Например, высказывая суждение «Семенов — адвокат», мы связываем понятия «Семенов» и «адвокат», отражая реальную связь между конкретным лицом и его признаком. В суждении «Владимир — брат Алексея» в связи понятий «Владимир» и «Алексей» выражены родственные отношения между двумя лицами. В суждении «В некоторых странах существует президентская форма правления» утверждается факт существования президентской формы правления в некоторых странах.